"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕГУЛЯРНОЕ ПРЕДСТАВЛЕНИЕЗначение РЕГУЛЯРНОЕ ПРЕДСТАВЛЕНИЕ в математической энциклопедии:
- 1) P. п. (левое) а л г е б р ы А - линейное представление Lалгебры Ав векторном пространстве Е=А, определяемое формулой L(a)b=ab для всех 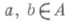 ; аналогично, формула ; аналогично, формула 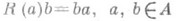 , определяет (анти)-представление алгебры Ав пространстве Е=А, наз. (правым) Р. п. А. Если А - топологич. алгебра (с умножением, непрерывным по совокупности переменных), то Lи R - непрерывные представления. Если А- алгебра с единицей или полупростая алгебра, то все ее Р. п.- точные. , определяет (анти)-представление алгебры Ав пространстве Е=А, наз. (правым) Р. п. А. Если А - топологич. алгебра (с умножением, непрерывным по совокупности переменных), то Lи R - непрерывные представления. Если А- алгебра с единицей или полупростая алгебра, то все ее Р. п.- точные.
2) Р. п. (п р а в о е) г р у п п ы G - линейное представление Rгруппы G в пространстве Екомплекснозначных функций на G, определенное формулой
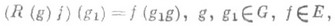
причем пространство Еравделяет точки группы G и обладает тем свойством, что функция 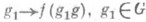 , принадлежит пространству Едля всех , принадлежит пространству Едля всех  . Аналогично, формула . Аналогично, формула
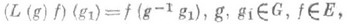
определяет (левое) Р. п. группы G в пространстве Е, если функция 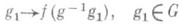 , принадлежит Едля всех , принадлежит Едля всех 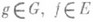 . Если G - топологич. группа, то в качестве пространства Ечасто рассматриваются пространства непрерывных функций на G. Если G - локально компактная группа, то (правым) Р. п. группы G наз. (правое) Р. п. группы G в пространстве L2(G), построенном по правоинвариантной мере Хаара на G; Р. п. локально компактной группы является ее непрерывным унитарным представлением, причем левое и правое Р. п. унитарно эквивалентны. А. И. Штерн. . Если G - топологич. группа, то в качестве пространства Ечасто рассматриваются пространства непрерывных функций на G. Если G - локально компактная группа, то (правым) Р. п. группы G наз. (правое) Р. п. группы G в пространстве L2(G), построенном по правоинвариантной мере Хаара на G; Р. п. локально компактной группы является ее непрерывным унитарным представлением, причем левое и правое Р. п. унитарно эквивалентны. А. И. Штерн.
|

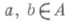 ; аналогично, формула
; аналогично, формула 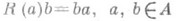 , определяет (анти)-представление алгебры Ав пространстве Е=А, наз. (правым) Р. п. А. Если А - топологич. алгебра (с умножением, непрерывным по совокупности переменных), то Lи R - непрерывные представления. Если А- алгебра с единицей или полупростая алгебра, то все ее Р. п.- точные.
, определяет (анти)-представление алгебры Ав пространстве Е=А, наз. (правым) Р. п. А. Если А - топологич. алгебра (с умножением, непрерывным по совокупности переменных), то Lи R - непрерывные представления. Если А- алгебра с единицей или полупростая алгебра, то все ее Р. п.- точные.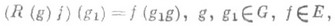
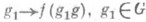 , принадлежит пространству Едля всех
, принадлежит пространству Едля всех  . Аналогично, формула
. Аналогично, формула 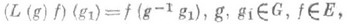
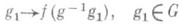 , принадлежит Едля всех
, принадлежит Едля всех 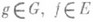 . Если G - топологич. группа, то в качестве пространства Ечасто рассматриваются пространства непрерывных функций на G. Если G - локально компактная группа, то (правым) Р. п. группы G наз. (правое) Р. п. группы G в пространстве L2(G), построенном по правоинвариантной мере Хаара на G; Р. п. локально компактной группы является ее непрерывным унитарным представлением, причем левое и правое Р. п. унитарно эквивалентны. А. И. Штерн.
. Если G - топологич. группа, то в качестве пространства Ечасто рассматриваются пространства непрерывных функций на G. Если G - локально компактная группа, то (правым) Р. п. группы G наз. (правое) Р. п. группы G в пространстве L2(G), построенном по правоинвариантной мере Хаара на G; Р. п. локально компактной группы является ее непрерывным унитарным представлением, причем левое и правое Р. п. унитарно эквивалентны. А. И. Штерн.