|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕГУЛЯРНОЕ КОЛЬЦОЗначение РЕГУЛЯРНОЕ КОЛЬЦО в математической энциклопедии: (в смысле Неймана) - ассоциативное кольцо (обычно с единицей), в к-ром уравнение Групповое кольцо группы G над Р. к. регулярно тогда и только тогда, когда любая конечно порожденная подгруппа в Gконечна и порядок каждой из таких подгрупп обратим в исходном Р. к. (см. [3]). Кольца эндоморфизмов всех свободных левых R-модулей регулярны в том и только в том случае, когда R классически полупросто [6]. Счетно порожденные односторонние идеалы Р. к. проективны [8]. Если Rесть Р. к., то конечно порожденные подмодули левого R-модуля Rn n -мерных строк над R образуют дедекиндову решетку Lс дополнениями, являющуюся подрешеткой решетки всех подмодулей модуля Rn. Решетка Lсодержит о д н о р о д н ы й б а з и с a1, . . ., an, то есть эти элементы независимы (см. Де-декиндова решетка), их сумма равна наибольшему элементу из L(а именно, Rn) и любые а i, и а j п е р с п е к т и в н ы, что означает существование для них общего дополнения. Наоборот, всякая дедекиндова решетка с дополнениями, обладающая однородным базисом, содержащим не менее четырех элементов, изоморфна решетке Lдля подходящего Р. к. R. Решетка Lизоморфна решетке главных левых идеалов кольца всех Важный частный случай Р. к.- с т р о г о р е г ул я р н о е к о л ь ц о, в к-ром, по определению, разрешимо уравнение Другой подкласс класса Р. к. образуют u-регулярные кольца, где, по определению, уравнение Р. к. наз. н е п р е р ы в н ы м с л е в а, если непрерывна решетка его главных левых идеалов. Непрерывное Р. к. u-регулярно и разлагается в прямую сумму строго Р. к. и самоинъективного кольца. На Р. к. может быть определена псевдоранг-функция, являющаяся аналогом меры на булевой алгебре. Она определяет псевдометрику. Пополнение Р. к. по этой метрике оказывается самоинъективным Р. к. (см. [8]). Р. к. являются частным случаем p-р е г у л я р н ы х к о л е ц, в к-рых, по определению, для каждого элемента анайдутся элемент хи натуральное число птакие, что Как двусторонний аналог Р. к. можно рассматривать б и р е г у л я р н ы е к о л ь ц а, в к-рых, по определению, каждый главный двусторонний идеал порождается центральным идемпотентом. Каждый двусторонний идеал бирегулярного кольца является пересечением его максимальных двусторонних идеалов. Всякое бирегулярное кольцо с единицей изоморфно кольцу глобальных сечений с бикомпактными носителями пучка простых колец с единицей над бикомпактным вполне несвязным хаусдорфовым топологич. пространством, п всякое такое кольцо глобальных сечений бирегулярно (см. [2]). В коммутативном случае классы бирегулярных, строго Р. к. и Р. к. совпадают, и простые кольца в последней теореме заменяются полями. Близки к Р. к. б э р о в с к и е к о л ь ц а, определяемые тем условием, что каждый левый (или, что при наличии единицы равносильно, каждый правый) аннулятор порождается идемпотентом. Примерами бэ-ровских колец служат кольцо эндоморфизмов векторного пространства над телом и кольцо ограниченных операторов гильбертова пространства. Бэровское кольцо наз. а б е л е в ы м, если все его идемпотенты центральны, и к о н е ч н ы м (п о Д е д е к и н д у), если xy=l влечет за собой ух=1. Идемпотент ебэровского кольца Rназ. а б е л е в ы м (к о н е ч н ы м), если кольцо еRе абелево (конечно по Дедекинду). Различаются следующие типы бэровских колец: Р. к. были введены для координатизации непрерывных геометрий, бирегулярные - в связи с исследованием функциональных представлений колец, бэровские (и риккатовы) - при исследовании колец операторов. Рассматривались неассоциативные Р. к. См. также *-регулярное кольцо, риккартово кольцо. Лит.:[1] Б у р б а к и Н., Коммутативная алгебра, пер. с франц., М., 1971; [2] Д а у н с Д ж., Г о ф м а н К., "Математика", 1968, т. 12, № 4, с. 3--24; [3]Л а м б е к Н., Кольца и модули, пер. с англ., М., 1971; [41 С к о р н я к о в Л. А., Дедекиндовы структуры с дополнениями и регулярные кольца, М., 1961; [5] Ф е й с К., Алгебра: кольца, модули и категории, пер. с англ., т. 1-2, М., 1977-79; [6] Цукерман Г. М., "Сиб. матем. ж.", 1966, т. 7, № 5, с. 1161-67; [7] Ш а й н Б. М., "Изв. ВУЗов. Математика", 1966, № 2, с. 111-22; [8] G о о d е а r 1 К. R., Von Neumann regular rings, L.- [a. o.], 1979; [9] К а р l a n s k y] I., Rings of operators, N. Y.- Amst., 1968; [10] N e u m a n n J., Continuous geometry, Princeton, 1960. Л. А. Скорняков. *-РЕГУЛЯРНОЕ КОЛЬЦО - регулярное кольцо, допускающее инволюционный антиавтоморфизм Лит.:[1] С к о р н я к о в Л. А., Дедекиндовы структуры с дополнениями и регулярные кольца, М., 1961; [2] В е r b е r i n a n S. К., Baer *-rings, В.- [а, о.], 1972; [3] К а р 1 a n s k у I., Rings of operators, N. Y.- Amst., 1968. Л. А. Скорняков. |
|
|
|

 разрешимо для любого а. Следующие свойства ассоциативного кольца R с единицей равносильны: а) R есть Р. к.; б) каждый главный левый идеал кольца R порождается идемпотентом; в) главные левые идеалы кольца Л образуют подрешетку в решетке всех его левых идеалов, являющуюся дедекиндовой решеткой с дополнениями; г) каждый главный левый идеал кольца Rимеет дополнение в структуре всех его левых идеалов; д) все левые R-модули плоские; е) имеют место правые аналоги свойств б) - д) (см. [3], [4], [5], [8], [10]).(Ввиду д) Р. к. иногда наз. а б с о л ю т н о п л о с к и м и. Коммутативное кольцо регулярно тогда и только тогда, когда инъективны все простые модули над ним (см. [5]). Любой конечно порожденный левый (правый) идеал Р. к. оказывается главным и, следовательно, выделяется прямым слагаемым. Всякий неделитель нуля в Р. к. обратим. Радикал Джекобсона Р. к. равен нулю. Кольцо матриц над Р. к. оказывается Р. к. Класс Р. к. замкнут относительно перехода к прямым произведениям и факторкольцам. Идеал Р. к. является Р. к. (возможно, без единицы). Если Р. к. нётерово или совершенно (слева или справа), то оно оказывается классически полупростым кольцом. Всякое классически полупростое кольцо регулярно. . Более того, регулярным оказывается кольцо эндоморфизмов векторного пространства над телом (даже бесконечномерного), а также факторкольцо кольца эндоморфизмов инъективного левого (правого) модуля над любым кольцом по его радикалу Джекобсона (см. [3]). В частности, всякое самоинъективное слева (справа) кольцо с нулевым радикалом Джекобсона регулярно.
разрешимо для любого а. Следующие свойства ассоциативного кольца R с единицей равносильны: а) R есть Р. к.; б) каждый главный левый идеал кольца R порождается идемпотентом; в) главные левые идеалы кольца Л образуют подрешетку в решетке всех его левых идеалов, являющуюся дедекиндовой решеткой с дополнениями; г) каждый главный левый идеал кольца Rимеет дополнение в структуре всех его левых идеалов; д) все левые R-модули плоские; е) имеют место правые аналоги свойств б) - д) (см. [3], [4], [5], [8], [10]).(Ввиду д) Р. к. иногда наз. а б с о л ю т н о п л о с к и м и. Коммутативное кольцо регулярно тогда и только тогда, когда инъективны все простые модули над ним (см. [5]). Любой конечно порожденный левый (правый) идеал Р. к. оказывается главным и, следовательно, выделяется прямым слагаемым. Всякий неделитель нуля в Р. к. обратим. Радикал Джекобсона Р. к. равен нулю. Кольцо матриц над Р. к. оказывается Р. к. Класс Р. к. замкнут относительно перехода к прямым произведениям и факторкольцам. Идеал Р. к. является Р. к. (возможно, без единицы). Если Р. к. нётерово или совершенно (слева или справа), то оно оказывается классически полупростым кольцом. Всякое классически полупростое кольцо регулярно. . Более того, регулярным оказывается кольцо эндоморфизмов векторного пространства над телом (даже бесконечномерного), а также факторкольцо кольца эндоморфизмов инъективного левого (правого) модуля над любым кольцом по его радикалу Джекобсона (см. [3]). В частности, всякое самоинъективное слева (справа) кольцо с нулевым радикалом Джекобсона регулярно. матриц над R (см. [4], [10]).
матриц над R (см. [4], [10]). . Равносильны следующие свойства Р. к. R: а) R строго регулярно; б) R не содержит ненулевых нильпотентных элементов; в) все идемпотенты кольца R центральны; г) каждый левый (или каждый правый) идеал кольца R является двусторонним; д) решетка главных левых (правых) идеалов кольца R дистрибутивна; е) мультипликативная полугруппа кольца R является инверсной полугруппой (см, [7], [8]).
. Равносильны следующие свойства Р. к. R: а) R строго регулярно; б) R не содержит ненулевых нильпотентных элементов; в) все идемпотенты кольца R центральны; г) каждый левый (или каждый правый) идеал кольца R является двусторонним; д) решетка главных левых (правых) идеалов кольца R дистрибутивна; е) мультипликативная полугруппа кольца R является инверсной полугруппой (см, [7], [8]). имеет в качестве решения обратимый элемент. В классе Р. к. u-регулярные кольца характеризуются транзитивностью перспективности в решетке конечно порожденных подмодулей суммы двух экземпляров основного кольца, а также возможностью сокращать прямую сумму на конечно порожденный проективный модуль (см. [4], [8]).
имеет в качестве решения обратимый элемент. В классе Р. к. u-регулярные кольца характеризуются транзитивностью перспективности в решетке конечно порожденных подмодулей суммы двух экземпляров основного кольца, а также возможностью сокращать прямую сумму на конечно порожденный проективный модуль (см. [4], [8]).
 - конечные кольца, содержащие абелев идемпотент, не принадлежащий никакому собственному прямому слагаемому;
- конечные кольца, содержащие абелев идемпотент, не принадлежащий никакому собственному прямому слагаемому;  - бесконечные по Дедекинду (т. е. не содержащие ненулевых конечных центральных идемпотентов) кольца, содержащие абелев идемпотент, не принадлежащий никакому собственному прямому слагаемому;
- бесконечные по Дедекинду (т. е. не содержащие ненулевых конечных центральных идемпотентов) кольца, содержащие абелев идемпотент, не принадлежащий никакому собственному прямому слагаемому;  (или
(или  ) - конечные по Дедекинду кольца без ненулевых абелевых идемпотентов, содержащие конечный идемпотент, не принадлежащий никакому собственному прямому слагаемому;
) - конечные по Дедекинду кольца без ненулевых абелевых идемпотентов, содержащие конечный идемпотент, не принадлежащий никакому собственному прямому слагаемому; 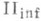 - бесконечные по Дедекинду кольца с условием, указанным в
- бесконечные по Дедекинду кольца с условием, указанным в  ;
;  - кольца без ненулевых конечных идемпотентов. Каждое бэровское кольцо единственным способом разлагается в прямую сумму колец перечисленных типов (см. [9]).
- кольца без ненулевых конечных идемпотентов. Каждое бэровское кольцо единственным способом разлагается в прямую сумму колец перечисленных типов (см. [9]). такой, что
такой, что  влечет за собой a=0. Идемпотент еил *-Р. к. наз. п р о е к ц и е й, если
влечет за собой a=0. Идемпотент еил *-Р. к. наз. п р о е к ц и е й, если  . Каждый левый (правый) идеал *-Р. к. порождается однозначно определенной проекцией. Поэтому можно говорить о решетке проекций *-Р. к. Если эта решетка полна, то она является непрерывной геометрией. Дедекиндова решетка с дополнениями, обладающая однородным базисом a1, . .., а n, где
. Каждый левый (правый) идеал *-Р. к. порождается однозначно определенной проекцией. Поэтому можно говорить о решетке проекций *-Р. к. Если эта решетка полна, то она является непрерывной геометрией. Дедекиндова решетка с дополнениями, обладающая однородным базисом a1, . .., а n, где  (см. Регулярное кольцо), является решеткой с ортодополнениями тогда и только тогда, когда она изоморфна решетке проекций нек-рого *-Р. к.
(см. Регулярное кольцо), является решеткой с ортодополнениями тогда и только тогда, когда она изоморфна решетке проекций нек-рого *-Р. к.