"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕГУЛЯРНОЕ КОЛЬЦО
Значение РЕГУЛЯРНОЕ КОЛЬЦО в математической энциклопедии:
в к о м м у т а т и в н о й а л г е б р е - нётерово кольцо А, все локализации 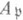 к-рого регулярны; здесь
к-рого регулярны; здесь 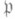 - простой идеал в А. При этом локальное нётерово кольцо Ас максимальным идеалом
- простой идеал в А. При этом локальное нётерово кольцо Ас максимальным идеалом 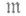 наз. р е г у л я р н ы м, если
наз. р е г у л я р н ы м, если 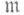 порождается пэлементами, где n=dim A, т. е. если касательное пространство
порождается пэлементами, где n=dim A, т. е. если касательное пространство 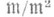 (как векторное пространство над полем вычетов) имеет размерность, равную dim А. Это равносильно отсутствию особенностей у схемы Spec A. Локальное Р. к. Авсегда целостно и нормально, а также факториально (т е о р е м а А у с л е н д е р а - Б у к с б а у м а), глубина его равна dim А. Ассоциированное градуированное кольцо
(как векторное пространство над полем вычетов) имеет размерность, равную dim А. Это равносильно отсутствию особенностей у схемы Spec A. Локальное Р. к. Авсегда целостно и нормально, а также факториально (т е о р е м а А у с л е н д е р а - Б у к с б а у м а), глубина его равна dim А. Ассоциированное градуированное кольцо
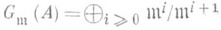
изоморфно кольцу многочленов  . Локальное нётерово кольцо Арегулярно тогда и только тогда, когда регулярно его пополнение
. Локальное нётерово кольцо Арегулярно тогда и только тогда, когда регулярно его пополнение 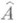 ; вообще, если АМ В - плоское расширение локальных колец и Врегулярно, то и Арегулярно. Для полных локальных Р. к. имеет место с т р у к т у р н а я т е о р е м а К о э н а: они имеют вид
; вообще, если АМ В - плоское расширение локальных колец и Врегулярно, то и Арегулярно. Для полных локальных Р. к. имеет место с т р у к т у р н а я т е о р е м а К о э н а: они имеют вид  , где R - поле или кольцо дискретного нормирования. Любой модуль конечного типа над локальным Р. к. обладает конечной свободной резольвентой (см. Гильберта теорема о сизигиях); верно и обратное (см. [2]).
, где R - поле или кольцо дискретного нормирования. Любой модуль конечного типа над локальным Р. к. обладает конечной свободной резольвентой (см. Гильберта теорема о сизигиях); верно и обратное (см. [2]).
Р. к. являются любое полей любое дедекиндово кольцо. Если Арегулярно, то регулярно кольцо многочленов A[X1, . . ., Х n]и кольцо формальных степенных рядов  над А. Если
над А. Если  - необратимый элемент локального Р. к., то А/ аА регулярно тогда и только тогда, когда
- необратимый элемент локального Р. к., то А/ аА регулярно тогда и только тогда, когда 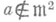
Лит.:[1] З а р и с с к и й О., С а м ю э л ь П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963; [2] С е р р Ж.- П., "Математика", 1963, т. 7, № 5, с. 3-93; [3] G r o t h e n d i е с k A., D i e u d o n n e J. (red.), Elements de geometrie algebrique, chap. 4, P., 1964. В. И. Данилов.

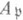 к-рого регулярны; здесь
к-рого регулярны; здесь 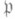 - простой идеал в А. При этом локальное нётерово кольцо Ас максимальным идеалом
- простой идеал в А. При этом локальное нётерово кольцо Ас максимальным идеалом 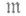 наз. р е г у л я р н ы м, если
наз. р е г у л я р н ы м, если 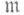 порождается пэлементами, где n=dim A, т. е. если касательное пространство
порождается пэлементами, где n=dim A, т. е. если касательное пространство 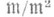 (как векторное пространство над полем вычетов) имеет размерность, равную dim А. Это равносильно отсутствию особенностей у схемы Spec A. Локальное Р. к. Авсегда целостно и нормально, а также факториально (т е о р е м а А у с л е н д е р а - Б у к с б а у м а), глубина его равна dim А. Ассоциированное градуированное кольцо
(как векторное пространство над полем вычетов) имеет размерность, равную dim А. Это равносильно отсутствию особенностей у схемы Spec A. Локальное Р. к. Авсегда целостно и нормально, а также факториально (т е о р е м а А у с л е н д е р а - Б у к с б а у м а), глубина его равна dim А. Ассоциированное градуированное кольцо 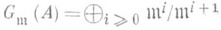
 . Локальное нётерово кольцо Арегулярно тогда и только тогда, когда регулярно его пополнение
. Локальное нётерово кольцо Арегулярно тогда и только тогда, когда регулярно его пополнение 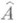 ; вообще, если АМ В - плоское расширение локальных колец и Врегулярно, то и Арегулярно. Для полных локальных Р. к. имеет место с т р у к т у р н а я т е о р е м а К о э н а: они имеют вид
; вообще, если АМ В - плоское расширение локальных колец и Врегулярно, то и Арегулярно. Для полных локальных Р. к. имеет место с т р у к т у р н а я т е о р е м а К о э н а: они имеют вид  , где R - поле или кольцо дискретного нормирования. Любой модуль конечного типа над локальным Р. к. обладает конечной свободной резольвентой (см. Гильберта теорема о сизигиях); верно и обратное (см. [2]).
, где R - поле или кольцо дискретного нормирования. Любой модуль конечного типа над локальным Р. к. обладает конечной свободной резольвентой (см. Гильберта теорема о сизигиях); верно и обратное (см. [2]). над А. Если
над А. Если  - необратимый элемент локального Р. к., то А/ аА регулярно тогда и только тогда, когда
- необратимый элемент локального Р. к., то А/ аА регулярно тогда и только тогда, когда