|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕГУЛЯРНАЯ ФУНКЦИЯ МНОЖЕСТВАЗначение РЕГУЛЯРНАЯ ФУНКЦИЯ МНОЖЕСТВА в математической энциклопедии: аддитивная функция m, определенная на системе множеств топологич. пространства, полная вариация к-рой где Свойство регулярности можно относить и к мере как частному случаю функции множества и говорить о р е г у л я р н о й м е р е, заданной на топологич. пространстве. Примером регулярной меры является Лебега мера. Лит.:[1] Д а н ф о р д Н., Ш в а р ц Д ж., Линейные операторы, пер. с англ., ч. 1, М., 1962; [2] А л е к с а н д р о в А. Д., "Матем. сб.", 1941, т. 9, с. 563-628. А. П. Терехин. |
|
|
|

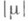 удовлетворяет условию
удовлетворяет условию 
 - внутренность множества
- внутренность множества  - замыкание множества F(E, G, F - из области определения m). Ограниченная аддитивная Р. ф. м., определенная на полукольце множеств бикомпактного топологич. пространства, является счетно аддитивной функцией (теорема Александрова).
- замыкание множества F(E, G, F - из области определения m). Ограниченная аддитивная Р. ф. м., определенная на полукольце множеств бикомпактного топологич. пространства, является счетно аддитивной функцией (теорема Александрова).