|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РЕГРЕССИОННЫЙ АНАЛИЗЗначение РЕГРЕССИОННЫЙ АНАЛИЗ в математической энциклопедии: - раздел математич. статистики, объединяющий практич. методы исследования регрессионной зависимости между величинами по статистич. данным (см. Регрессия). Проблема регрессии в математич. статистике характерна тем, что о распределениях изучаемых величин нет достаточной информации. Пусть, напр., имеются основания предполагать, что случайная величина Yимеет нек-рое распределение вероятностей при фиксированном значении хдругой величины, так что где b - совокупность неизвестных параметров, определяющих функцию g(x), и нужно по результатам наблюдений определить значения параметров. В зависимости от природы задачи и целей анализа результаты эксперимента Исследование регрессии по экспериментальным данным производится методами, основанными на принципах средней квадратич. регрессии. Р. а. решает следующие основные задачи: 1) выбор модели регрессии, что заключает в себе предположения о зависимости функций регрессии от x и b, 2) оценка параметров b в выбранной модели методом наименьших квадратов, 3) проверка статистич. гипотез о регрессии. Наиболее естественной с точки зрения единого метода оценки неизвестных параметров является модель регрессии, линейная относительно этих параметров: Выбор функций gi(x)иногда определяется по расположению экспериментальных значений ( х, у )на диаграмме рассеяния, чаще - теоретич. соображениями. Предполагается также, что дисперсия s2 результатов наблюдений постоянна (или пропорциональна известной функции от x). Стандартный метод оценки регрессии основан на использовании многочлена нек-рой степени или в простейшем случае - линейной функции (линейная регрессия) Существуют критерии линейности и рекомендации по выбору степени аппроксимирующего многочлена. В соответствии с принципами средней квадратич. регрессии оценка неизвестных регрессии коэффициентовb0, . . ., bm и дисперсии s2 осуществляется методом наименьших квадратов. Согласно этому методу в качестве статистич. оценок параметров b0, . . ., bm выбираются такие значения Многочлен где Случайные величины Если дисперсия зависит от х, то метод наименьших квадратов применим с нек-рыми видоизменениями. Если изучается зависимость случайной величины Yот нескольких переменных где где матрица Аизвестна, но эта схема сводится к модели (*). Несмещенной оценкой b по методу наименьших квадратов является величина а смещенной оценкой для s2 служит Модель (*) является наиболее общей линейной моделью, поскольку она применима к различным регрессионным ситуациям и включает в себя все виды параболической регрессии Y по Указанный метод построения эмпирич. регрессии в предположении нормального распределения результатов наблюдений приводит к оценкам для b и s2, совпадающим с оценками наибольшего правдоподобия. Однако оценки, полученные этим методом, являются в нек-ром смысле наилучшими и в случае отклонения от нормальности, если только объем выборки достаточно велик. В данной матричной форме общая линейная модель регрессии (*) допускает простое обобщение на тот случай, когда наблюдаемые величины Задачи Р. а. не ограничиваются построением точечных оценок параметров b и s2 общей линейной модели (*). Проблема точности построенной эмпирич. зависимости наиболее эффективно разрешается при допущении, что вектор наблюдений подчиняется Стьюдента распределению с n-kстепенями свободы. Этот факт используется для построения доверительных интервалов для параметров bi- и для проверки гипотез о значениях, к-рые принимает величина bi. Кроме того, появляется возможность найти доверительные интервалы для Р. а. является одним из наиболее распространенных методов обработки экспериментальных данных при изучении зависимостей в физике, биологии, экономике, технике и др. областях. На моделях Р. а. основаны такие разделы математич. статистики, как дисперсионный анализ и планирование эксперимента, эти модели широко используются в многомерном статистическом анализе. Лит.:[1] К е н д а л л М. Д ж., С т ь ю а р т А., Статистические выводы и связи, пер. с англ., М., 1973; [2] С м и рн о в Н. В., Д у н и н - Б а р к о в с к и й Н. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; [3] А й в а з я н С. А., Статистическое исследование зависимостей, М., 1968; [4] Р а о С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968; [5] Д р е й п е р Н., С м и т Г., Прикладной регрессионный анализ, пер. с англ., М., 1973. А. В. Прохоров. |
|
|
|

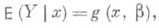
 по-разному интерпретируются в отношении переменной х. Для установления связи между величинами в эксперименте используется модель, основанная на упрощенных допущениях: величина хявляется контролируемой величиной, значения к-рой заранее задаются при планировании эксперимента, а наблюдаемые значения
по-разному интерпретируются в отношении переменной х. Для установления связи между величинами в эксперименте используется модель, основанная на упрощенных допущениях: величина хявляется контролируемой величиной, значения к-рой заранее задаются при планировании эксперимента, а наблюдаемые значения 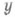 представимы в виде
представимы в виде  где величины ei характеризуют ошибки, независимые при различных измерениях и одинаково распределенные с нулевым средним и постоянной дисперсией. В случае неконтролируемой переменной результаты наблюдений (x1 у1,), . . ., ( х п, у п )представляют собой выборку из нек-рой двумерной совокупности. Методы Р. а. одинаковы и в том, и в другом случае, однако интерпретация результатов различается (в последнем случае анализ существенно дополняется методами теории корреляции).
где величины ei характеризуют ошибки, независимые при различных измерениях и одинаково распределенные с нулевым средним и постоянной дисперсией. В случае неконтролируемой переменной результаты наблюдений (x1 у1,), . . ., ( х п, у п )представляют собой выборку из нек-рой двумерной совокупности. Методы Р. а. одинаковы и в том, и в другом случае, однако интерпретация результатов различается (в последнем случае анализ существенно дополняется методами теории корреляции).



 , к-рые обращают в минимум выражение
, к-рые обращают в минимум выражение 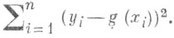
 , построенный методом наименьших квадратов, наз. э м п и р и ч е с к о й л и н и е й р е г р е с с и и и является статистич. оценкой неизвестной истинной линии регрессии. При гипотезе линейности регрессии уравнение эмпирич. прямой регрессии имеет вид
, построенный методом наименьших квадратов, наз. э м п и р и ч е с к о й л и н и е й р е г р е с с и и и является статистич. оценкой неизвестной истинной линии регрессии. При гипотезе линейности регрессии уравнение эмпирич. прямой регрессии имеет вид 

 наз. в ы б о р о ч н ы м и к о э ф ф и ц и е н т а м и р е г р е с с и и. Несмещенная оценка параметра s2 дается формулой
наз. в ы б о р о ч н ы м и к о э ф ф и ц и е н т а м и р е г р е с с и и. Несмещенная оценка параметра s2 дается формулой 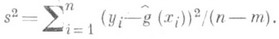
 , то общую линейную модель регрессии удобнее записывать в матричной форме: вектор наблюдений ус независимыми компонентами
, то общую линейную модель регрессии удобнее записывать в матричной форме: вектор наблюдений ус независимыми компонентами  имеет среднее значение и ковариационную матрицу
имеет среднее значение и ковариационную матрицу  (*)
(*) - вектор коэффициентов регрессии,
- вектор коэффициентов регрессии, 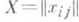 , i=1, . . ., п, j=1 ,. . ., k, - матрица известных величин, связанных друг с другом, вообще говоря, произвольным образом, I - единичная матрица n-го порядка; при этом
, i=1, . . ., п, j=1 ,. . ., k, - матрица известных величин, связанных друг с другом, вообще говоря, произвольным образом, I - единичная матрица n-го порядка; при этом  . В более общем случае допускается корреляция между наблюдениями
. В более общем случае допускается корреляция между наблюдениями  :
:
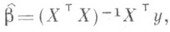

 (в частности, рассмотренная выше параболич. регрессия Y по хпорядка тможет быть сведена к модели (*), в к-рой трегрессионных переменных функционально связаны). При таком линейном понимании Р. а. задача оценки р и вычисления ковариационной матрицы оценок
(в частности, рассмотренная выше параболич. регрессия Y по хпорядка тможет быть сведена к модели (*), в к-рой трегрессионных переменных функционально связаны). При таком линейном понимании Р. а. задача оценки р и вычисления ковариационной матрицы оценок 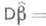
 сводится к задаче обращения матрицы
сводится к задаче обращения матрицы 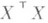 .
. являются векторными случайными величинами. При атом никакой новой статистич. задачи не возникает (см. Регрессии матрица).
являются векторными случайными величинами. При атом никакой новой статистич. задачи не возникает (см. Регрессии матрица). распределен нормально. Если вектор
распределен нормально. Если вектор  распределен нормально и любая оценка
распределен нормально и любая оценка  является линейной функцией от
является линейной функцией от  , можно заключить, что величина
, можно заключить, что величина  распределена нормально со средним bi и дисперсией
распределена нормально со средним bi и дисперсией 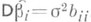 , где bii- диагональный элемент матрицы
, где bii- диагональный элемент матрицы  . Кроме того, оценка s2 для s2 распределена независимо от любой компоненты вектора
. Кроме того, оценка s2 для s2 распределена независимо от любой компоненты вектора  а величина
а величина  имеет ". хи- квадрат" распределение с( п-k )степенями свободы. Отсюда следует, что статистика
имеет ". хи- квадрат" распределение с( п-k )степенями свободы. Отсюда следует, что статистика 
 при фиксированных значениях всех регрессионных переменных и доверительные интервалы, содержащие следующее (n+1)-е значение величины
при фиксированных значениях всех регрессионных переменных и доверительные интервалы, содержащие следующее (n+1)-е значение величины  (т. н. интервалы предсказания). Наконец, можно на основе вектора выборочных коэффициентов регрессии
(т. н. интервалы предсказания). Наконец, можно на основе вектора выборочных коэффициентов регрессии  построить доверительный эллипсоид для вектора b или для любой совокупности неизвестных коэффициентов регрессии, а также доверительную область для всей линии или прямой регрессии.
построить доверительный эллипсоид для вектора b или для любой совокупности неизвестных коэффициентов регрессии, а также доверительную область для всей линии или прямой регрессии.