|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАЦИОНАЛЬНАЯ ФУНКЦИЯЗначение РАЦИОНАЛЬНАЯ ФУНКЦИЯ в математической энциклопедии: 1) Р. ф.- функция w=R(z), где R(z) - рациональное выражение от z, т. е. выражение, полученное из независимого переменного z и нек-рого конечного набора чисел (действительных или комплексных) посредством конечного числа арифметич. действий. Р. ф. можно записать (не единственным образом) в виде где Р, Q - многочлены, Р. ф. степени ( т, п).при n=0, т. е. многочлен, наз. ц е л о й р а ц и о н а л ь н о й ф у н к ц и е й, в противном случае - д р о б н о - р а ц и о н а л ь н о й ф у н к ц и е й. Р. ф. где Р 1 -многочлен, наз. целой частью дроби Р/Q, a P2/Q- правильная дробь. Правильная дробь с несократимой записью R(z)=P (z)/Q(z), где может быть единственным образом разложена в сумму простейших дробей: Если P(x)/Q(x)-- правильная Р. ф. с действительными коэффициентами и где где все коэффициенты действительны. Эти коэффициенты, как и Р. ф. степени (m, п).в несократимой записи определена и аналитична в расширенной комплексной плоскости (т. е. плоскости, дополненной точкой В результате арифметич. действий над. Р. ф. получают также Р. ф. (деление на и произвольной постоянной С(здесь числа Удобные для вычислений, Р. ф. используются для приближенного представления функций. Рассматриваются также Р. ф. от нескольких действительных или комплексных переменных R = P/Q, где Р, Q - многочлены от соответствующих переменных где Ф 1, Ф 2, ... - линейно независимая система непрерывных функций на нек-ром бикомпакте X, а A1,..., А т, B1, . . ., B п - числа. См. также Дробно-линейная функция, Жуковского функция. Лит.:[1] П р и в а л о в И. И., Введение в теорию функций комплексного переменного, 12 изд., М., 1977; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд., М., 1975. Е. П. Долженко. 2)Р. ф. н а а л г е б р а и ч е с к о м м н о г о о бр а з и и - обобщение классич. понятия рациональной функции (см. п. 1). Р. ф. на неприводимом алгебраич. многообразии X - это класс эквивалентности пар (U, f), где X- непустое открытое подмножество в X, а f - регулярная функция на U. Две пары (U, f) и (V, g )наз. эквивалентными, если f=g на В случае, когда X=Spec R - аффинное неприводимое многообразие, поле Р. ф. на Xсовпадает с полем частных кольца R. Степень трансцендентности над kполя k(X). наз. р а з м е р н о с т ь ю м н о г о о бр а з и я X. Лит.:[1] Ш а ф а р е в и ч И. Р., Основы алгебраической геометрии, М., 1972. Вик. С. Куликов. |
|
|
|

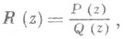
 . Коэффициенты этих многочленов наз. к о э ф ф и ц и е н т а м и Р. ф. Дробь P/Qназ. несократимой, если Р, Q не имеют общих нулей (то есть Р, Q - взаимно простые многочлены). Всякую Р. ф. можно записать в виде несократимой дроби R(z)=P(z)/Q(z);если при этом Р имеет степень m, a Q - степень п, то степенью Р. ф. R(z)наз. пару (m, n) или число
. Коэффициенты этих многочленов наз. к о э ф ф и ц и е н т а м и Р. ф. Дробь P/Qназ. несократимой, если Р, Q не имеют общих нулей (то есть Р, Q - взаимно простые многочлены). Всякую Р. ф. можно записать в виде несократимой дроби R(z)=P(z)/Q(z);если при этом Р имеет степень m, a Q - степень п, то степенью Р. ф. R(z)наз. пару (m, n) или число 
 не имеет степени. При m<n дробь Rназ. правильной, при
не имеет степени. При m<n дробь Rназ. правильной, при  - неправильной. Неправильную дробь можно единственным образом записать в виде
- неправильной. Неправильную дробь можно единственным образом записать в виде 
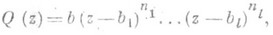
 (1)
(1)
 - действительные числа,
- действительные числа, , то P(x)/Q(x)также единственным образом представляется в виде
, то P(x)/Q(x)также единственным образом представляется в виде  (2)
(2) в (1), могут быть найдены неопределенных коэффициентов методом.
в (1), могут быть найдены неопределенных коэффициентов методом. ) за исключением конечного числа особых точек- полюсов в нулях ее знаменателя, а при т>п еще и в точке
) за исключением конечного числа особых точек- полюсов в нулях ее знаменателя, а при т>п еще и в точке 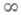 ; при этом сумма кратностей полюсов функции Rравна ее степени N. Обратно, всякая аналитич. ция, имеющая в расширенной комплексной плоскости в качестве особых точек только полюсы, является Р. ф.
; при этом сумма кратностей полюсов функции Rравна ее степени N. Обратно, всякая аналитич. ция, имеющая в расширенной комплексной плоскости в качестве особых точек только полюсы, является Р. ф. исключается), так что все Р. ф. образуют поле; вообще, Р. ф. с коэффициентами из нек-рого поля образуют поле. Если R1(z), R2(z) суть Р. ф., то и R1(R2(z))является Р. ф. Производная порядка рот Р. ф. степени N есть Р. ф. степени
исключается), так что все Р. ф. образуют поле; вообще, Р. ф. с коэффициентами из нек-рого поля образуют поле. Если R1(z), R2(z) суть Р. ф., то и R1(R2(z))является Р. ф. Производная порядка рот Р. ф. степени N есть Р. ф. степени 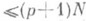 . Неопределенный интеграл (первообразная) от Р. ф. представляет собой сумму нек-рой Р. ф. и выражений вида
. Неопределенный интеграл (первообразная) от Р. ф. представляет собой сумму нек-рой Р. ф. и выражений вида  . Если Р. ф. R(х)действительна при действительном х, то неопределенный интеграл может быть записан в виде суммы нек-рой Р.
. Если Р. ф. R(х)действительна при действительном х, то неопределенный интеграл может быть записан в виде суммы нек-рой Р. ф. R0(x)с действительными коэффициентами, выражений вида
ф. R0(x)с действительными коэффициентами, выражений вида 
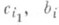 ,
, 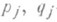 - те же, что и в (2), Mj, Nj - нек-рые действительные числа). Функцию R0(x)по Остроградского методу можно найти, минуя разложение R(х)на простейшие дроби (2).
- те же, что и в (2), Mj, Nj - нек-рые действительные числа). Функцию R0(x)по Остроградского методу можно найти, минуя разложение R(х)на простейшие дроби (2). , а также абстрактные Р. ф.
, а также абстрактные Р. ф.
 . Р. ф. на Xобразуют поле, обозначаемое k(X).
. Р. ф. на Xобразуют поле, обозначаемое k(X).