|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛЗначение РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ в математической энциклопедии: - раздел теории чисел, в к-ром изучаются закономерности распределения простых чисел (п. ч.) среди натуральных чисел. Центральной является проблема наилучшего асимптотич. выражения при О с н о в н а я т е о р е м а а р и ф м е т и к и: каждое натуральное число n>1 является или п. ч. или единственным (с точностью до перестановки сомножителей) произведением п. ч. (т. н. к а н о н и ч е с к о е п р е д с т а в л е н и е числа п), где Для нахождения п. ч. от 1 до хслужит известный с 3 в. до н. э. метод Эратосфена решета. Решето Эратосфена является простейшей процедурой получения последовательности п. ч. Однако аналитич. ормула решета где dпробегает делители произведения всех п. ч. Рассмотрение последовательности п. ч. от 1 до х:2,3, 5, 7, 11, 14, ..., р(1) показывает, что с увеличением x она становится в среднем все более редкой. Существуют сколь угодно длинные отрезки ряда натуральных чисел, среди к-рых нет ни одного п. ч. Напр., п-1 натуральных чисел вида п!+2, ... , п!+п для любого Первый результат о величине p(х).-т е о р е м а Е в к л и д а: где ряд распространяется на все натуральные числа, а произведение на все п. ч. Тождество (3) и его обобщения играют фундаментальную роль в теории Р. п. ч. Исходя из него, Л. Эйлер доказал, что ряд и, в то же время, почти все натуральные числа являются составными, т. к. Далее значительного успеха достиг П. Л. Чебышев (1851-52, см. [2]). Он доказал, что: 1) для любых т>0, М>0 есть последовательности 2) если существует предел частного к-рая служит наилучшим приближением для p(х). Затем П. Л. Чебышев установил истинный порядок роста p(х), т. е. существование постоянных а>0, А>0 таких, что причем, а=0,92... , А=1,05... для в к-ром введенная П. Л. Чебышевым функция y определяется суммой по степеням р т, m=1, 2, ... , п. ч. р: Именно, комбинация вследствие (5), дает тождество из к-рого следует, что Отсюда, вследствие асимптотич. формулы Стирлинга для n, вытекает аналог неравенств (4) для y(x), из к-рых частичным суммированием получаются неравенства (4). Функция Чебышева y (х)оказалась более удобной, чем p(х), при изучении Р. п. ч., поскольку наилучшим приближением ее является сам аргумент х. По-этому обычно сначала рассматривают y (х), а затем частичным суммированием получают соответствующий результат для p(х). Принцип Римана. В 1859-60 Б. Риман (В. Riemann, см. [3]) рассмотрел введенную Л. Эйлером для s>l функцию Вместо формулы Римана обычно используется более простой конечный ее аналог для y(x), доказанный (наряду с формулой Римана) X. Мангольдтом (Н. Маngoldt, 1895). Именно, для x>1 где r=b+ig пробегает нетривиальные нули Поскольку формула (6) показывает, что величина разности y(x)-x в главном определяется величиной b (действительной частью самых правых нулей r). В частности, если Наоборот, из этих соотношений следует, что Причем эти соотношения существенно усилить нельзя, т. е. существуют последовательности Таким образом, согласно принципу Римана проблема асимптотич. выражения функции Р. п. ч. y(x), p(х). сводится к проблеме границы действительной части нетривиальных нулей функции Методы Адамара и Валле Пуссена. Асимптотич. закон Р. п. ч. в простейшем виде был получен в 1896 независимо Ж. Адамаром (J. Hadamard) и Ш. Bалле Пуссеном (Ch. La Vallee Poussin), к-рые доказали, что при постоянных a>0, b>0. Были получены также дальнейшие расширения области свободной от нулей функции z(s) (см. [4] - [12]). Метод Вейля - Литлвуда. Существует определенная связь между ростом модуля функции z(s) и ее нулями вблизи прямой s=1. Именно, если При этом для оценки z(s) используется частная сумма ее ряда (2), к-рая сводит вопрос к оценке тригонометрич. сумм вида За счет оценок таких сумм по Вейля методу Дж. Литлвуд (J. Littlewood, 1921) показал, что для Отсюда Метод Виноградова. Дальнейший прогресс в оценках p(x), y(x). связан с созданием И. М. Виноградовым (см. Виноградова метод).нового, значительно более мощного метода оценок тригонометрич. сумм. При помощи этого метода им в 1938 было доказано, что z(s)№0. при В 1858 И. М. Виноградов и другие (см. [6] -[11]) показали, что z(s)№0 при Это пока (1983) лучший результат о границе нетривиальных нулей функции z(s), к-рому отвечает лучший результат в Р. п. ч.: Из асимптотики p(х)следует асимптотика n-го простого числа для Элементарные методы. Так называют методы изучения асимптотич. закона Р. п. ч., не опирающиеся на принцип Римана (нули дзета-функции) и, вообще, на какие бы то ни было положения теории функций комплексного переменного. Впервые такой метод открыли в 1948 А. Сельберг [16] и П. Эрдёш [17]. В основе лежит элементарная ф о р м у л а С е л ь б е р г а Дальнейшая задача состоит в том, чтобы из асимптотики в среднем для В 1970 X. Дайамонд и Дж. Стейниг (см. [19]) существенно усовершенствовали идею и технику оценок элементарного метода и доказали, что для Наконец, в 1973 А. Ф. Лаврик и А. Ш. Собиров [20] показали, что при элементарном методе доказательства справедлива теорема: для Этот результат представляет пока лучшее достижение элементарного метода в изучении Р. п. ч., хотя он несколько слабее того, к-рый получен аналитич. методом, в принципе эти результаты близки между собой. Разность между простыми числами. Существует много вопросов Р. п. ч., касающихся разности между п. ч. Среди них выделяются вопросы поведения Спомощью гипотезы Римана доказано, что Лучшей к 1983 является оценка Кроме этого, за счет оценок И. М. Виноградова тригонометрич. сумм с п. ч. (см. Виноградова метод).доказано круговым методом (см. [13]), что если положить то при любых фиксированных А>1, М>0 Отсюда, в частности, следует, что при Х = хlog - Ax. для всех Аналогичные результаты получены для систем п. ч. Простые числа арифметической прогрессии. Первый способ (Евклида) доказательства бесконечности числа п. ч. можно перенести и на нек-рые арифметич. прогрессии. Но доказать таким путем, что в каждой арифметич. прогрессии dn+l, первый член к-рой l и разность dвзаимно просты, содержится бесконечно много п. ч., до сих пор (1983) не удалось. Задачу другим методом решил П. Дирихле (P. Dirichlet, 1837-40), распространив идею Л. Эйлера о том, что В случае фиксированного значения а вследствие оценки К. Зигеля (К. Siegel, 1935) для любого фиксированного А>1 при где j(d) - функция Эйлера, а- положительная постоянная, с 1=с 1(A) - неэффективная постоянная >0, то есть c1 не может быть вычислена по заданному А . Если справедлива расширенная Римана гипотеза, то для Таким образом, к 1983 доказано, что п. ч. равномерно распределены по всем j(d)прогрессиям Метод решета Бруна, как и его модификация, предложенная А. Сельбергом в 1947, показывает, что для всех с абсолютной константой Выражение для y (х; d, l)no принципу Римана через нули r=b+ig лежащие в полосе L(s, c), имеет вид где штрих у суммы - знак суммирования по комплексным c mod d, a - действительный нуль функции L(s,c), если он существует и больше Т- любое Из (8) видно, если не считать слагаемого, отвечающего а, что остаточный член асимптотики y (x; d, l )определяется величиной двойной суммы, зависящей и от действительной части нулей r и от количества всех L(s, c) с c mod d, имеющих нули Таким образом, понижение разного рода оценок для п. ч. связывается не только с отсутствием нулей L (s, c) в критич. полосе, но и с сравнительно редким их распределением здесь. Реализация этой идеи была одним из центральных направлений исследований Р. п. ч. последних 40 лет. Начало положил Ю. В. Линник открытием в 1941 метода большого решета (см. [22], а также [14], [15], [24]). Особо важными являются теоремы о наименьшем п. ч. в арифметической прогрессии, о поведении p (х; d, l )и y (х; d, l )в среднем по Именно, в 1944 Ю. В. Линник [23] показал, что при В 1965 А. И. Виноградов и Э. Бомбьери независимо получили сильные оценки сумм N2 из (9). Более совершенствованный метод оценки этих сумм разработал Г. Монтгомери (Н. Montgomery, 1969). Одним из следствий оценок N2 является следующий результат о Р. п. ч. в арифметич. прогрессиях в среднем: при любом постоянном Другие вопросы распределения простых чисел. Пусть где определяется рядами, зависящими от h, m, d и n. Э. Ландау (Е. Landau, 1903-1918) перенес нек-рые результаты Р. п. ч. на алгебраические числовые поля. Пусть К - алгебраическое числовое поле n-й степени, p (х; К) - есть число простых идеалов с нормой где с - абсолютная положительная постоянная, и где W - отрицание символа о (малое). Много изучалась функция F(x, у), обозначающая число натуральных чисел Лит.:[1] Э й л е р Л., Введение в анализ бесконечных, пер. с латин., 2 изд., т. 1, М., 1961; [2] Ч е б ы ш е в П. Л., Избр. матем. труды, М.- Л., 1946; [3] Р и м а н Б., Соч., пер. с нем., М.- Л., 1948; [4] И н г а м А. Е., Распределение простых чисел, пер. с англ., М.- Л., 1936; [5] В и н о г р ад о в И. М., Избр. труды, М., 1952; [6] е г о ж е, "Изв. АН СССР. Сер. матем.", 1958, т. 22, № 2, с. 161-64; [7] е г о ж е, Метод тригонометрических сумм в теории чисел, М., 1971; [8] Т и т ч м а р ш Е., Теория дзета-функции Римана, пер. с англ., М., 1953; [9] II р а х а р К., Распределение простых чисел, пер. с нем., М., 1967; [10] К а р а ц у б а А. А., Основы аналитической теории чисел, М., 1975; [11] X у а Л о-к е н, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М.. 1964; [12] Ч у д а к о в Н. Г., Введение в теорию L функций Дирихле, М.- Л., 1947; [13] Л а в р и к А. Ф. "Тр. Матем. ин-та АН СССР", 1961, т. 64, с. 90-125; [14] Д э в е н п о р т Г., Мультипликативная теория чисел, пер. с англ., М.. 1971; [15] М о н т г о м е р и Г., Мультипликативная теория чисел, пер. с англ., М., 1974; [16] S е l b е г g A., "Ann. Math.", 1949, v. 50, p. 305-13; [17] Е г d o s P., "Proc. Nat. Acad. Sci. USA", 1949, v. 35, p. 371-84; [18] Л а в р и к А. Ф. (Обзорный доклад международной конференции по теории чисел, М., 1981); [19] D i a m o n d Н. G., S t е i n i g J., "Invent. Math.", 1970, V. 11, p. 199-258; [20] Л а в р и к А. Ф., С о б и р о в А. Ш., "Докл. АН СССР", 1973, т. 211, № 3, с. 534-36; [21] R o s s e r В., "Proc. London math. Soc.", 1939, v. 45 (2), p. 21-44; [22] Л и н н и к Ю. В., "Докл. АН СССР", 1941, т. 30, № 4, с. 290-92; [23] е г о ж е, "Матем. сб.", 1944, т. 15, с. 139-78; [24] Л а в р и к А. Ф., "Успехи матем. наук", 1980, т. 35, в. 2, с. 55-65; [25] H a l b e r s t a m Н., R i с h е г t Н. Е., Sieve Methods, L.- [etc], 1974. А. Ф. Лаврик. |
|
|
|

 функции p(х), обозначающей число п. ч., не превосходящих х, а также функции p(х; d, l), обозначающей число п. ч., не превосходящих хв арифметич. прогрессии dn+l при
функции p(х), обозначающей число п. ч., не превосходящих х, а также функции p(х; d, l), обозначающей число п. ч., не превосходящих хв арифметич. прогрессии dn+l при 
 , для растущих вместе с хзначений d.
, для растущих вместе с хзначений d.
 - различные п. ч., n1, ...... ,
- различные п. ч., n1, ...... ,  - натуральные числа. Таким образом, п. ч. есть базис мультипликативного построения ряда натуральных чисел, это, однако, непосредственно ничего не говорит о величине p(х).
- натуральные числа. Таким образом, п. ч. есть базис мультипликативного построения ряда натуральных чисел, это, однако, непосредственно ничего не говорит о величине p(х).
 ,
,  - число простых делителей
- число простых делителей  - целая часть и, непригодна для изучения p (х).при
- целая часть и, непригодна для изучения p (х).при 
 являются составными числами. В то же время в (1) встречаются п. ч. такие, как 8004119 и 8004121, разность между к-рыми равна 2 (п. ч.- близнецы). Проблема поведения p(x) при
являются составными числами. В то же время в (1) встречаются п. ч. такие, как 8004119 и 8004121, разность между к-рыми равна 2 (п. ч.- близнецы). Проблема поведения p(x) при  является одной из наиболее трудных и интересных проблем теории чисел.
является одной из наиболее трудных и интересных проблем теории чисел. при
при  . Л. Эйлер (L. Еu1ег, 1737, 1749, см. [1]) ввел функцию
. Л. Эйлер (L. Еu1ег, 1737, 1749, см. [1]) ввел функцию  (2) и показал, что при
(2) и показал, что при 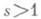
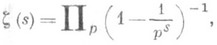 (3)
(3) и произведение по простым ррасходятся. Это - новое доказательство
и произведение по простым ррасходятся. Это - новое доказательство 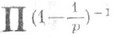 бесконечности числа п. ч. Более того, Л. Эйлер установил, что п. ч. "много", ибо
бесконечности числа п. ч. Более того, Л. Эйлер установил, что п. ч. "много", ибо 

 , для к-рых
, для к-рых 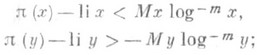
 при
при  , то он равен 1. Тем самым впервые был решен вопрос о существовании простой функции
, то он равен 1. Тем самым впервые был решен вопрос о существовании простой функции 
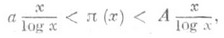 (4)
(4) . Он же доказал, что при любом
. Он же доказал, что при любом  в интервале ( п, 2п).содержится по крайней мере одно п. ч. (п о с т у л а т Б е р т р а н а). В основе вывода неравенств (4) лежит т о ж д е с т в о Ч е б ы ш е в а
в интервале ( п, 2п).содержится по крайней мере одно п. ч. (п о с т у л а т Б е р т р а н а). В основе вывода неравенств (4) лежит т о ж д е с т в о Ч е б ы ш е в а  (5)
(5)
 для
для 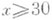 в форме
в форме 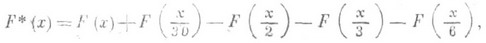

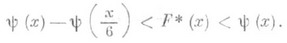
 как функцию комплексного переменного
как функцию комплексного переменного  , где s, t - действительные переменные, определяемую рядом (2) при s>1 (см. Дзета-функция), и обнаружил исключительную важность этой функции для теории Р. п. ч. В частности, он указал выражение разности p(х)- li хчерез хи нули функции
, где s, t - действительные переменные, определяемую рядом (2) при s>1 (см. Дзета-функция), и обнаружил исключительную важность этой функции для теории Р. п. ч. В частности, он указал выражение разности p(х)- li хчерез хи нули функции 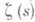 , лежащие в полосе
, лежащие в полосе 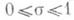 , к-рые наз. н е т р и в и а л ьн ы м и н у л я м и ф у н к ц и и z,(s).
, к-рые наз. н е т р и в и а л ьн ы м и н у л я м и ф у н к ц и и z,(s). (6)
(6) , Т - любое
, Т - любое 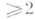

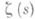
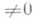 правее вертикали s=q,
правее вертикали s=q,  , для функций y(x), p(x) справедливы следующие асимптотич. выражения:
, для функций y(x), p(x) справедливы следующие асимптотич. выражения:
 для
для  . Если справедлива гипотеза Римана, т. <е. все нетривиальные нули
. Если справедлива гипотеза Римана, т. <е. все нетривиальные нули  лежат на одной прямой
лежат на одной прямой  , тогда асимптотич. закон распределения п. ч. должен иметь вид
, тогда асимптотич. закон распределения п. ч. должен иметь вид 
 такие, что
такие, что 
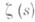 . До сих пор (1983), однако, не удалось найти какое-либо постоянное q,
. До сих пор (1983), однако, не удалось найти какое-либо постоянное q,  , с условием
, с условием 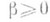 . Искомая граница для b оказывается связанной с мнимой частью g нулей r, причем так, что прямая s=1 является для нее асимптотой.
. Искомая граница для b оказывается связанной с мнимой частью g нулей r, причем так, что прямая s=1 является для нее асимптотой.
 , т. е. что на прямой s=-1 нет нулей функции
, т. е. что на прямой s=-1 нет нулей функции  . В 1899 Ш. Bалле Пуссен показал, что
. В 1899 Ш. Bалле Пуссен показал, что  (s+it)№0 в области
(s+it)№0 в области  Тем самым было доказано, что
Тем самым было доказано, что 
 при
при  , где j (t),1/q (t) - положительные неубывающие функции
, где j (t),1/q (t) - положительные неубывающие функции  такие, что
такие, что  при
при  , то существует постоянная Атакая, что z(s)№0 в области
, то существует постоянная Атакая, что z(s)№0 в области 


 при
при 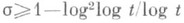 и, следовательно, z(s)№0 в области
и, следовательно, z(s)№0 в области 

 и соответственно что
и соответственно что 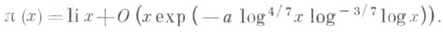


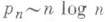 . Показано (см. [21] ) также, что р n> >n log nдля всех
. Показано (см. [21] ) также, что р n> >n log nдля всех 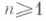 и что для
и что для 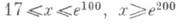



 (7)
(7) в виде (7) вывести асимптотику
в виде (7) вывести асимптотику  Это можно сделать по-разному, но общим во всех случаях является использованием факта медленного колебания функции
Это можно сделать по-разному, но общим во всех случаях является использованием факта медленного колебания функции  (см. [18]). В 1962 Э. Бомбьери (Е. Воmbieri) и Э. Вирзинг (Е. Wirsing) доказали, что при любом фиксированном А>0
(см. [18]). В 1962 Э. Бомбьери (Е. Воmbieri) и Э. Вирзинг (Е. Wirsing) доказали, что при любом фиксированном А>0
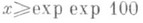
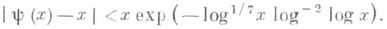


 -
-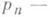 разности между соседними п. ч.; проблема количества п. ч. близнецов, или, более общо, пар п. ч. разности 2k и, вообще, числа систем р, p+ul ... , р+и т из m+1 п. ч., лежащих на отрезке [1, х].
разности между соседними п. ч.; проблема количества п. ч. близнецов, или, более общо, пар п. ч. разности 2k и, вообще, числа систем р, p+ul ... , р+и т из m+1 п. ч., лежащих на отрезке [1, х].
 , а нек-рые эвристич. рассуждения показывают, что, вероятно, справедлива оценка
, а нек-рые эвристич. рассуждения показывают, что, вероятно, справедлива оценка 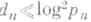
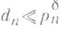 , где
, где 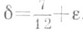 , e>0, полученная М. Н. Хаксли (М. N. Huxley, 1973) по методу большого решета. Что касается пар п. ч. разности, равной 2 (близнецов), или разности, равной 2k, k=1,2, ... , то до сих пор (1983) неизвестно, является количество их бесконечным или нет. Пусть
, e>0, полученная М. Н. Хаксли (М. N. Huxley, 1973) по методу большого решета. Что касается пар п. ч. разности, равной 2 (близнецов), или разности, равной 2k, k=1,2, ... , то до сих пор (1983) неизвестно, является количество их бесконечным или нет. Пусть 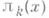 есть число пар п. ч., не превосходящих х, разности 2k. В1919 В. Брун (V. Вrun) нашел метод решета (см. Вруна решето), к-рый позволил получить ожидаемую оценку сверху для
есть число пар п. ч., не превосходящих х, разности 2k. В1919 В. Брун (V. Вrun) нашел метод решета (см. Вруна решето), к-рый позволил получить ожидаемую оценку сверху для  :
:


 , исключая не более
, исключая не более 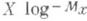 из них,
из них, 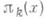 имеет асимптотич. выражение в виде
имеет асимптотич. выражение в виде 
 при любом
при любом 
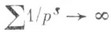 при
при  на п. ч.
на п. ч. . Для этого он ввел арифметич. функции - характеры c=c(n, d) (см. Дирихле характер).и функции L(s,c). (см. Дирихле L-функция), которые подобно функции z(s) для p(х), y (х)служат в качестве основного аппарата изучения функции p (х; d, l )и ее аналога
. Для этого он ввел арифметич. функции - характеры c=c(n, d) (см. Дирихле характер).и функции L(s,c). (см. Дирихле L-функция), которые подобно функции z(s) для p(х), y (х)служат в качестве основного аппарата изучения функции p (х; d, l )и ее аналога 
 , большинство результатов, указанных выше для p(x) y(х), перенесены и на функции p(х; d, l)и y (х; d, l). Однако особый интерес здесь представляют результаты для растущих вместе с хзначений d, к-рые важны в аддитивной теории чисел и ряде других задач. В таком случае возникают значительные дополнительные трудности, связанные прежде всего с оценкой величины d - наибольшего действительного нуля функции L(s,c) по mod d. При помощи Пейджа теорем доказано, что для
, большинство результатов, указанных выше для p(x) y(х), перенесены и на функции p(х; d, l)и y (х; d, l). Однако особый интерес здесь представляют результаты для растущих вместе с хзначений d, к-рые важны в аддитивной теории чисел и ряде других задач. В таком случае возникают значительные дополнительные трудности, связанные прежде всего с оценкой величины d - наибольшего действительного нуля функции L(s,c) по mod d. При помощи Пейджа теорем доказано, что для 




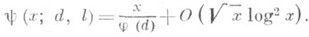

 , разности dлишь при
, разности dлишь при  . Что же касается отрезков прогрессий
. Что же касается отрезков прогрессий  разности, напр. d=xe с каким бы то ни было постоянным e>0, то из предыдущего не следует даже, что такая прогрессия содержит хотя бы одно п. ч. l
разности, напр. d=xe с каким бы то ни было постоянным e>0, то из предыдущего не следует даже, что такая прогрессия содержит хотя бы одно п. ч. l , имеет место неравенство сверху
, имеет место неравенство сверху 
 , но никаких оценок снизу для p(х; d, l )эти методы дать но могут.
, но никаких оценок снизу для p(х; d, l )эти методы дать но могут.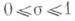 функции
функции 
 ,
,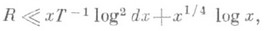

 . Если для
. Если для  через N (s, T, c) обозначить число нулей функции L(s, c) в прямоугольнике:
через N (s, T, c) обозначить число нулей функции L(s, c) в прямоугольнике:  , то вопросы оценки остаточного члена для y (х; d, l )и его среднего значения сводятся к вопросам оценки плотности распределения нулей L-функций в виде
, то вопросы оценки остаточного члена для y (х; d, l )и его среднего значения сводятся к вопросам оценки плотности распределения нулей L-функций в виде  (9)
(9) и о двойном усреднении этих функций по
и о двойном усреднении этих функций по 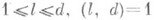 , и
, и  .
. сумма N1 в (9) имеет оценку
сумма N1 в (9) имеет оценку 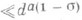 , где а - постоянная; отсюда он вывел существование постоянной стакой, что любая арифметич. прогрессия dn+l, где
, где а - постоянная; отсюда он вывел существование постоянной стакой, что любая арифметич. прогрессия dn+l, где 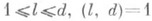 , содержит п. ч., меньшее dc. Последняя к 1983 оценка постоянной Линника имеет вид с=17; а если верна плотностная гипотеза:
, содержит п. ч., меньшее dc. Последняя к 1983 оценка постоянной Линника имеет вид с=17; а если верна плотностная гипотеза: 
 , то
, то 

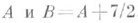 . Эти оценки существенно усилить уже нельзя, т. к. из расширенной гипотезы Римана следует, что B = A + 2.
. Эти оценки существенно усилить уже нельзя, т. к. из расширенной гипотезы Римана следует, что B = A + 2. есть количество чисел вида
есть количество чисел вида 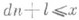 , к-рые являются произведением простых n чисел. X. Рихерт (Н. Pichert, 1953) доказал, что
, к-рые являются произведением простых n чисел. X. Рихерт (Н. Pichert, 1953) доказал, что 

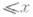 в К. Тогда
в К. Тогда 

 , не содержащих простых делителей, меньших у. Для
, не содержащих простых делителей, меньших у. Для 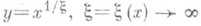 при
при  , такие числа наз. к в а з и п р о с т ы м и ч и с л а м и. Методом решета для этих чисел получена достаточно полная теория их распределения, аналогичная ожидаемой теории Р. п. ч. Рассматривалось также распределение чисел с малыми простыми делителями (см. [25]).
, такие числа наз. к в а з и п р о с т ы м и ч и с л а м и. Методом решета для этих чисел получена достаточно полная теория их распределения, аналогичная ожидаемой теории Р. п. ч. Рассматривалось также распределение чисел с малыми простыми делителями (см. [25]).