|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАСПРЕДЕЛЕНИЕ ДРОБНЫХ ДОЛЕЙ МНОГОМЕРНОЕЗначение РАСПРЕДЕЛЕНИЕ ДРОБНЫХ ДОЛЕЙ МНОГОМЕРНОЕ в математической энциклопедии: - распределение в n-мерном единичном кубе Последовательность дробных долей {Pj}, j=1, 2, ... , наз. р а в н о м е р н о р а с п р е д е л е н н о й в единичном n-мерном кубе Е, если для каждого прямоугольника V, содержащегося в E, имеет место равенство где jm,(V)- число точек среди первых тчленов последовательности {Pj}, попавших в V, и Последовательность Р j, j=1, 2, ... , точек n-мерного пространства наз. р а в н о м е р н о р а с п р е д ел е н н о й п о м о д у л ю 1, если соответствующая ей последовательность дробных долей {Pj}равномерно распределена в единичном кубе Е . Критерий Вейля для Р. д. д. м. Последовательность {Pj}, j=1, 2, ... , равномерно распределена в единичном кубе Етогда и только тогда, когда для каждого набора целых чисел (а 1, a2, ... , an)№0, 0. . .0). Частным случаем этой теоремы является Вейля критерий для равномерного распределения по модулю 1 последовательности действительных чисел. Из критерия Вейля следует т е о р е м а К р о н е к е р а: пусть q1, q2, ... , qn, 1 - действительные числа, линейно независимые над полем рациональных чисел, al, a2, ... , an - произвольные действительные числа и N,e - положительные числа; тогда существуют целые ти p1, р 2,... , р n такие, что для всех i=l, 2, ... , п. Иначе говоря, последовательность mq=(mq1, mq2 ... , тq п), m=1,2, ... , равномерно распределена по модулю 1. Лит.; [1] К а с с е л с Д ж. В. С., Введение в теорию диофантовых приближений, пер. с англ., М., 1961. С. А. Степанов. |
|
|
|
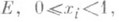i=1,2, .... п, дробных долей 
последовательности точек n-мерного евклидова пространства 
, j-1, 2, ... . Здесь { } - знак дробной доли.
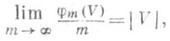
- мера прямоугольника V.
