"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БИГАРМОНИЧЕСКАЯ ФУНКЦИЯ
Значение БИГАРМОНИЧЕСКАЯ ФУНКЦИЯ в математической энциклопедии:
функция  действительных переменных, определенная в области
действительных переменных, определенная в области  евклидова пространства
евклидова пространства  ,
,  , имеющая непрерывные частные производные до 4-го порядка включительно и удовлетворяющая в
, имеющая непрерывные частные производные до 4-го порядка включительно и удовлетворяющая в  уравнению
уравнению

где D -оператор Лапласа. Это уравнение наз. бигарионическим уравнением. Класс Б. ф. включает класс гармонических функций и является подклассом класса полигармонических функций. Каждая Б. ф. есть аналитич. функция от координат  .
.
Наибольшее значение с точки зрения приложений имеют Б. ф.  двух переменных. Такие Б. ф. представимы при помощи гармонич. функций
двух переменных. Такие Б. ф. представимы при помощи гармонич. функций  или
или  в виде
в виде

или

где  - постоянная. Основная краевая задача для Б. <ф. состоит в следующем: найти Б. ф. в области
- постоянная. Основная краевая задача для Б. <ф. состоит в следующем: найти Б. ф. в области  , непрерывную вместе с производными 1-го порядка в замкнутой области
, непрерывную вместе с производными 1-го порядка в замкнутой области  и удовлетворяющую на границе Сусловиям
и удовлетворяющую на границе Сусловиям

где  - производная по нормали к
- производная по нормали к  - заданные непрерывные функции дуги
- заданные непрерывные функции дуги  на контуре С. Указанные выше представления Б. ф. позволяют получить решение задачи (*) в явном виде в случае круга D, исходя из интеграла Пуассона для гармонич. функций (см. [1]).
на контуре С. Указанные выше представления Б. ф. позволяют получить решение задачи (*) в явном виде в случае круга D, исходя из интеграла Пуассона для гармонич. функций (см. [1]).
Б. <ф. двух переменных допускают также представление

при помощи двух аналитич. функций 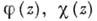 комплексного переменного
комплексного переменного  . Это представление позволяет свести краевую задачу
. Это представление позволяет свести краевую задачу  для произвольной области
для произвольной области  к системе краевых задач для аналитич. функций, метод решения к-рой подробно разработан Г. В. Колосовым и Н. И. Мусхелишвили. Эта методика получила развитие при решении различных плоских задач теории упругости, в к-рых основной Б. ф. является функция напряжений, или Эйри функция (см. [2], [3]).
к системе краевых задач для аналитич. функций, метод решения к-рой подробно разработан Г. В. Колосовым и Н. И. Мусхелишвили. Эта методика получила развитие при решении различных плоских задач теории упругости, в к-рых основной Б. ф. является функция напряжений, или Эйри функция (см. [2], [3]).
Лит.:[1] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966, гл. 4; [2] Мусхелишвили Н. И., Некоторые основные задачи математической теории упругости, 5 изд., М., 1966, гл. 2; [3] Лаврентьев М. А., Ша6ат Б. В., Методы теории функций комплексного переменного, 3 изд., М., 1965.
Е. Д. Соломенцев.

 действительных переменных, определенная в области
действительных переменных, определенная в области  евклидова пространства
евклидова пространства  ,
,  , имеющая непрерывные частные производные до 4-го порядка включительно и удовлетворяющая в
, имеющая непрерывные частные производные до 4-го порядка включительно и удовлетворяющая в  уравнению
уравнению
 .
. двух переменных. Такие Б. ф. представимы при помощи гармонич. функций
двух переменных. Такие Б. ф. представимы при помощи гармонич. функций  или
или  в виде
в виде

 - постоянная. Основная краевая задача для Б. <ф. состоит в следующем: найти Б. ф. в области
- постоянная. Основная краевая задача для Б. <ф. состоит в следующем: найти Б. ф. в области  , непрерывную вместе с производными 1-го порядка в замкнутой области
, непрерывную вместе с производными 1-го порядка в замкнутой области  и удовлетворяющую на границе Сусловиям
и удовлетворяющую на границе Сусловиям 
 - производная по нормали к
- производная по нормали к  - заданные непрерывные функции дуги
- заданные непрерывные функции дуги  на контуре С. Указанные выше представления Б. ф. позволяют получить решение задачи (*) в явном виде в случае круга D, исходя из интеграла Пуассона для гармонич. функций (см. [1]).
на контуре С. Указанные выше представления Б. ф. позволяют получить решение задачи (*) в явном виде в случае круга D, исходя из интеграла Пуассона для гармонич. функций (см. [1]).
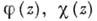 комплексного переменного
комплексного переменного  . Это представление позволяет свести краевую задачу
. Это представление позволяет свести краевую задачу  для произвольной области
для произвольной области  к системе краевых задач для аналитич. функций, метод решения к-рой подробно разработан Г. В. Колосовым и Н. И. Мусхелишвили. Эта методика получила развитие при решении различных плоских задач теории упругости, в к-рых основной Б. ф. является функция напряжений, или Эйри функция (см. [2], [3]).
к системе краевых задач для аналитич. функций, метод решения к-рой подробно разработан Г. В. Колосовым и Н. И. Мусхелишвили. Эта методика получила развитие при решении различных плоских задач теории упругости, в к-рых основной Б. ф. является функция напряжений, или Эйри функция (см. [2], [3]).