|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАНГЗначение РАНГ в математической энциклопедии: линейного обыкновенного дифференциального уравнения в комплексной области - число r=k+1, где Коэффициенты уравнения (1) - сходящиеся при больших Понятие Р. употребляется только тогда, когда Понятие Р. уравнения и особой точки используется при исследовании структуры решений уравнения (1) на бесконечности. Пусть Q(z) - многочлен степени р, - формальный ряд, наз. н о р м а л ь н ы м (соответственно п о д н о р м а л ь н ы м) порядка Порядок нормального (поднормального) решения не превосходит Р. уравнения; это верно, и для формальных решений вида (2). Если ранг rуравнения (1) целый, то оно имеет по крайней море одно формальное решение вида (2) порядка r. Подстановка У р а в н е н и е м Г а м б у р г е р а наз. уравнение (1) с рациональными коэффициентами, если оно имеет ровно две особые точки: регулярную z=0 и иррегулярную Понятие Р. вводится и в том случае, когда уравнение (1) имеет конечную особую точку (см. [2], [3]). В случае линейной системы из n обыкновенных дифференциальных уравнений в комплексной области где Лит.:[1] P o i n c a r e H., "Acta math.", 1886, v. 8; [2] А й н с Э. Л., Обыкновенные дифференциальные уравнения, пер. с англ., Харьков, 1939; [3] Л а т ы ш е в а К. Я., Тер е щ е н к о Н. И., О р е л Г. С., Нормально-регулярные решения и их приложения, К., 1974; [4] К о д д и н г т о н Э., Л е-в и н с о н Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [5] К а м к е Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [6] В а з о в В., Асимптотические разложения решений обыкновенных дифференциальных уравнений, пер. с англ., М., 1968. М. В. Федорюк. |
|
|
|

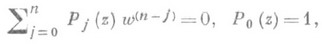 (1)
(1)
 ряды
ряды 

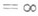 - особая точка дифференциального уравнения (1). Р. дифференциального уравнения наз. также р а н г о м о с о б о й т о ч к и
- особая точка дифференциального уравнения (1). Р. дифференциального уравнения наз. также р а н г о м о с о б о й т о ч к и 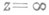 . Если эта точка - регулярная особая точка, то r=0; если иррегулярная особая точка, то r>0. Число kназ. п о д р а н г о м. Р. уравнения - целое или дробное число. Если подранг дробный, со знаменателем
. Если эта точка - регулярная особая точка, то r=0; если иррегулярная особая точка, то r>0. Число kназ. п о д р а н г о м. Р. уравнения - целое или дробное число. Если подранг дробный, со знаменателем  , то подранг уравнения, полученного из (1) заменой переменной
, то подранг уравнения, полученного из (1) заменой переменной  , будет целым. Р. уравнения инвариантен относительно замены переменной вида
, будет целым. Р. уравнения инвариантен относительно замены переменной вида  , где функция
, где функция  голоморфна и отлична от нуля в точке
голоморфна и отлична от нуля в точке 

 - целое число. Ряд
- целое число. Ряд  (2)
(2) , если s= 1 (соответственно
, если s= 1 (соответственно 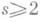 ). Решение уравнения (1), представимое сходящимся в окрестности точки
). Решение уравнения (1), представимое сходящимся в окрестности точки  нормальным (поднормальным) рядом, наз. н о р м а л ь н ы м (п о д н о рм а л ь н ы м) решением того же порядка (см. [2], [3]).
нормальным (поднормальным) рядом, наз. н о р м а л ь н ы м (п о д н о рм а л ь н ы м) решением того же порядка (см. [2], [3]).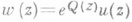 не меняет Р. уравнения. Если подранг
не меняет Р. уравнения. Если подранг  , где р, q - взаимно простые целые числа и
, где р, q - взаимно простые целые числа и  , то уравнение имеет не менее qформальных решений вида (2) порядка r.
, то уравнение имеет не менее qформальных решений вида (2) порядка r. . Для уравнения Гамбургера получены достаточные условия, при к-рых оно имеет нормальные решения, а при п=2 - необходимые и достаточные условия существования нормальных и поднормальных решений (см. [2]).
. Для уравнения Гамбургера получены достаточные условия, при к-рых оно имеет нормальные решения, а при п=2 - необходимые и достаточные условия существования нормальных и поднормальных решений (см. [2]). (3)
(3) -целое число, матрица-функция A(z) голоморфна в точке
-целое число, матрица-функция A(z) голоморфна в точке  и
и  , число r+1 наз. р а н-г о м с и с т е м ы (3), или р а н г о м о с о б о й т о ч к и
, число r+1 наз. р а н-г о м с и с т е м ы (3), или р а н г о м о с о б о й т о ч к и  , число r - ее п о д р а н г о м (см. [4] - [6]). Если
, число r - ее п о д р а н г о м (см. [4] - [6]). Если  , то точка
, то точка  - регулярная особая точка; в отличие от скалярного уравнения (1), точка
- регулярная особая точка; в отличие от скалярного уравнения (1), точка  может быть регулярной особой, если
может быть регулярной особой, если 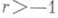 (см. [4]).
(см. [4]).