" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

БИБЕРБАХА МНОГОЧЛЕНЫ

Значение БИБЕРБАХА МНОГОЧЛЕНЫ в математической энциклопедии:

экстремальные многочлены, приближающие функцию, к-рая отображает конформно данную односвязную область на круг. Впервые были рассмотрены Л. Бибербахом, [1] в связи с задачей о приближенном вычислении конформно отображающей функции.

Пусть односвязная область Gрасположена в конечной части плоскости и ограничена кривой Г, а функция отображает эту область конформно и однолистно на круг 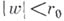при условиях 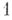, где - произвольная фиксированная точка области и зависит от 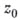. Многочлен , минимизирующий интеграл

в классе всех многочленов степени 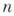при условиях 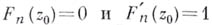, наз. многочленом Бибербаха. В классе всех функций, аналитических в области Gи удовлетворяющих тем же условиям, этот интеграл минимизируется отображающей функцией 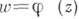. Если контур 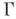- жорданова кривая, то последовательность 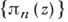сходится к функции 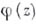равномерно внутри области G. В замкнутой области 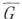сходимости может и не быть (см. [2]). Если же контур Г удовлетворяет нек-рым дополнительным условиям гладкости, то последовательность 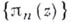сходится равномерно в замкнутой области, причем скорость сходимости зависит от степени гладкости кривой Г.

Лит.:[1] Bieberbach L., Circolo mat. Palermo", v. 38, 1914, p. 98-112: [2] Келдыш М. В., "Матем. сб.", 1939, т. 5(47), в. 2, с. 391-401; [3] Мергелян С. Н., Некоторые вопросы конструктивной теории функций, М., 1951; [4] Суетин П. К., "Тр. матем. ин-та АН СССР", 1971, т. 100.

П. К. Суетин.