|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАЗМЕЩЕНИЕЗначение РАЗМЕЩЕНИЕ в математической энциклопедии: с повторениями из_m элементов по п - конечная последовательность а = =(ai1, ai2,...,ain).элементов нек-рого множества А ={а 1,а2,...,а т}. Если все члены а различны, то аназ. Р. без повторений. Число всех возможных Р. с повторениями из тпо правно т n, а без повторений - (т) п=т( т -1). . .( т-п-1). Р. можно рассматривать как функцию j, заданную на Если говорят, что все ячейки одинаковы, то имеют в виду, что Р. разбиваются на классы так, что два Р., определяемые функциями Если не различать как частицы, так и ячейки, то получают размещение подинаковых частиц по тодинаковым ячейкам; число таких Р. равно Рассматриваются и другие разбиения Р. на классы, напр, когда вышеупомянутые подстановки Лит.:[1] С а ч к о в В. Н., Комбинаторные методы дискретной математики, М., 1977; [2] Р и о р д а н Д ж., Введение в комбинаторный анализ, пер. с англ., М., 1963. В. М. Михеев. |
|
|
|
={1, 2, . . ., п}и принимающую значения из А:j (k=)aik,k=1,2,. . ., п. Элементы Апринято называть ячейками (или урнами), а элементы 
- частицами (или шарами); j определяет заполнение различных ячеек различными частицами. Если речь идет о неразличимых частицах или ячейках, то подразумевается, что рассматриваются классы Р. Так, если все частицы одинаковы, то два Р., определяемые соответственно функциям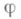и 
и 
, относятся к одному классу, если найдется подстановка s множества 
такая, что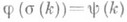 
для всех 
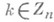В этом случае число таких классов, или, как говорят, число размещений подинаковых частиц по тразличным ячейкам, есть число сочетаний с повторениями из ппо т.
и 
соответственно, относятся к одному классу, если существует подстановка 
множества А, при к-рой 
для всех 
. В этом случае число размещений n различных частиц по тодинаковым ячейкам, т. е. число классов, равно 
, где S( п, k) - ч и с л а Стирлинга II рода:
, где pn(k) - число разбиений пна kнатуральных слагаемых.
и 
берутся из подгрупп симметрич. групп соответственно степеней n и т(см. об этом и других обобщениях в [1], [2]). Синонимами "Р." являются термины "n-перестановка", "упорядоченная n-выборка из генеральной совокупности".