|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАЗМЕРНОСТИ ТЕОРИЯЗначение РАЗМЕРНОСТИ ТЕОРИЯ в математической энциклопедии: - часть топологии, в к-рой для каждого компакта, а впоследствии и для более общих классов топологич. пространств тем или иным естественным образом определяется числовой топологич. инвариант - размерность, совпадающий, если Xесть полиэдр (в частности, многообразие), с его числом измерений в смысле элементарной или дифференциальной геометрии. Первое общее определение размерности было дано Л. Брауэром (L. Brouwer, 1913) для компактов и даже более широкого класса полных метрич. пространств. Определение строится по индукции следующим образом. Пустому множеству приписывается размерность - 1. В предположении, что определены пространства, а значит и лежащие в них множества, размерности Совершенно иной подход к понятию размерности берет начало от А. Лебега (Н. Lebesgue), высказавшего следующую теорему: n-мерный в смысле элементарной геометрии куб Qn при любом положительном числе e может быть покрыт конечным числом замкнутых множеств (даже кубов) диаметра <e таким образом, что кратность этого покрытия равна n+1, тогда как при достаточно малом e>0 не существует покрытия куба Qn, к-рое имеет кратность <n+1 и состоит из замкнутых множеств диаметра <e (при этом кратностью какой-либо (конечной) совокупности множеств наз. наибольшее целое число ттакое, что в данной совокупности имеется тмножеств с непустым пересечением). Теперь можно теорему Лебега сформулировать так. Число измерений куба Qn есть наименьшее такое целое число n, для к-рого имеется сколь угодно мелкое (т. е. состоящее из элементов сколь угодно малого диаметра) покрытие кратности n+1 замкнутыми множествами. Эта теорема, впервые доказанная лишь Л. Брауэром, приводит к следующему определению. Размерностью dim Xкомпакта X(определенной посредством покрытий) наз. наименьшее число птакое, что при любом e>0 компакт Xимеет покрытие кратности n+1, состоящее из замкнутых множеств диаметра При определении размерности компакта Xприменяется понятие диаметра множества, относящееся к метрике, а не к топологии компакта X. Однако доказывается, что определенное так число dim Xтем не менее является топологич. инвариантом компакта X, т. е. что два гомеоморфные между собою компакта имеют одну и ту же размерность dim X. Этот факт устанавливается непосредственно, но его легко вывести и из того, что числу dim Xможно дать и непосредственно топологич. определение, опирающееся лишь на топологию компакта X. П о к р ы т и е м данного топологич. пространства наз. любая конечная совокупность его открытых множеств, дающих в своей сумме все это пространство. Покрытие a' мельче покрытия a, если a' вписано в a, т. е. если каждый элемент покрытия a' является подмножеством хотя бы одного элемента покрытия a. Оказывается, размерность dim Xможно определить так: число dim Xесть наименьшее целое число птакое, что для всякого покрытия пространства Xсуществует вписанное в него покрытие кратности n + 1. Но это определение, очевидно, может быть сформулировано не только для компактов, а для любых топологич. пространств, и позволяет определить для них размерность. Размерность dim X, определенная таким образом для топологич. пространств, позволяет построить содержательную и богатую математич. фактами теорию, оставаясь, по крайней мере, в классе нормальных пространств (а значит, в частности) и метризуемых пространств). Одной из главных проблем Р. т. является выяснение наиболее широких условий, в к-рых имеет место т. н. основное тождество Урысона, а именно: ind X = Ind X = dim.X. Оказывается, оно имеет место для всех сепарабельных метризуемых пространств, т. е. для всех нормальных пространств со счетной базой, а также для пространств локально бикомпактных групп (теорема П а с ы н к о в а). Без предположения сепарабельности для метризуемых пространств можно утверждать лишь справедливость формулы Катетова а для бикомпактов - формулы Александрова причем имеются бикомпакты X, для к-рых (пример Л у н ц а-Л о к у ц и е в с к о г о), и бикомпакты X, для к-рых (пример Ф и л и п п о в а). Большое общепознавательное значение имеет следующая теорема Нёбелинга - Понтрягина: необходимое и достаточное условие для того, чтобы топологич. пространство Xбыло гомеоморфно подпространству какого-либо евклидова пространства конечного числа измерений, заключается в том, чтобы Xбыло нормальным пространством конечной размерности, имеющим счетную базу. Это позволяет при изучении конечномерных компактов и вообще конечномерных нормальных пространств со счетной базой рассматривать их как подпространства евклидовых пространств. В связи с этим приобретает особый интерес т. н. теорема об e-с д в и г а х: для того чтобы компакт X, лежащий в каком-либо евклидовом пространстве Одной из важнейших теорем Р. т. является т. н. теорема о существенных отображениях, лежащая в основе значительной части всей этой теории. Пусть f - непрерывное отображение (нормального) пространства Xна n-мерный шар Qn с границей Sn-1. Пусть Теорема о существенных отображениях лежит в основе т. н. гомологической теории размерности, позволяющей применить к изучению размерности в весьма общих предположениях методы алгебраич. топологии. Понятие гомологической размерности связано с понятиями цикла и гомологии и поэтому предполагает, что наряду с топологич. пространством Xдана и нек-рая коммутативная группа После этого можно определить гомологич. размерность компакта Xпо группе коэффициентов Если от циклов и гомологии перейти к коциклам и когомологиям, то получится когомологическая размерность, причем когомологич. размерность компакта по данной дискретной группе Лит. см. при ст. Размерность. П. С. Александров. |
|
|
|

 , говорят, что пространство Xимеет размерность
, говорят, что пространство Xимеет размерность  , если между любыми двумя дизъюнктными замкнутыми множествами Аи В пространства Xимеется перегородка Ф размерности
, если между любыми двумя дизъюнктными замкнутыми множествами Аи В пространства Xимеется перегородка Ф размерности  (при этом перегородкой между множествами A и В в пространстве Xназ. такое замкнутое множество Ф этого пространства, что дополнение
(при этом перегородкой между множествами A и В в пространстве Xназ. такое замкнутое множество Ф этого пространства, что дополнение  есть сумма двух дизъюнктных открытых множеств Си D, из к-рых одно содержит множество А, а другое - множество В). В 1921 П. С. Урысон и К. Менгер (К. Menger) независимо от Л. Брауэра и друг от друга пришли к эквивалентному в случае компактов и даже любых сепарабельных метрич. пространств определению, отличающемуся от брауэровского тем, что одно из двух замкнутых множеств А, Впредполагается состоящим из одной точки. Определения размерности в смысле Брауэра и в смысле Урысона и Менгера могут быть сформулированы для любых хаусдорфовых пространств, и определяемые ими топологич. инварианты наз. соответственно большой и малой индуктивной размерностями и обозначаются Ind Xи ind X, причем всегда
есть сумма двух дизъюнктных открытых множеств Си D, из к-рых одно содержит множество А, а другое - множество В). В 1921 П. С. Урысон и К. Менгер (К. Menger) независимо от Л. Брауэра и друг от друга пришли к эквивалентному в случае компактов и даже любых сепарабельных метрич. пространств определению, отличающемуся от брауэровского тем, что одно из двух замкнутых множеств А, Впредполагается состоящим из одной точки. Определения размерности в смысле Брауэра и в смысле Урысона и Менгера могут быть сформулированы для любых хаусдорфовых пространств, и определяемые ими топологич. инварианты наз. соответственно большой и малой индуктивной размерностями и обозначаются Ind Xи ind X, причем всегда 
 . Не меняя содержания этого определения, можно заменить в его формулировке замкнутые множества открытыми.
. Не меняя содержания этого определения, можно заменить в его формулировке замкнутые множества открытыми.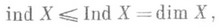

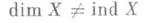

 , имел размерность
, имел размерность  , необходимо и достаточно, чтобы при любом e>0 этот компакт мог быть превращен в полиэдр размерности
, необходимо и достаточно, чтобы при любом e>0 этот компакт мог быть превращен в полиэдр размерности  посредством e-сдвига в пространстве
посредством e-сдвига в пространстве  (при этом e-сдвигом подпространства Xв евклидовом пространстве
(при этом e-сдвигом подпространства Xв евклидовом пространстве  наз. такое непрерывное отображение f этого подпространства Xв содержащее его евклидово пространство
наз. такое непрерывное отображение f этого подпространства Xв содержащее его евклидово пространство  , при к-ром расстояние r ( х, fx).любой точки
, при к-ром расстояние r ( х, fx).любой точки  от ее образа fx меньше числа e). Интуитивное содержание этой теоремы состоит в том, что всякий компакт данной коночной размерности п, рассматриваемый как множество, лежащее в каком-либо евклидовом пространстве
от ее образа fx меньше числа e). Интуитивное содержание этой теоремы состоит в том, что всякий компакт данной коночной размерности п, рассматриваемый как множество, лежащее в каком-либо евклидовом пространстве  , может быть сколь угодно малым непрерывным видоизменением (к чему и сводится его e-сдвиг) превращен в полиэдр той же, но не меньшей, размерности. Эта теорема так же, как и определение размерности dim Xдля компактов, может быть переформулирована в чисто топологич. терминах, причем снова "сколь угодно малые" числа e>0 заменяются "сколь угодно мелкими" покрытиями w. Это позволяет аналогичную теорему сформулировать для любых нормальных пространств и придти к заключению, что в некром (все же наглядном) геометрическом смысле всякое n-мерное нормальное пространство "похоже" и даже "сколь угодно мало отличается" от n-мерного полиэдра.
, может быть сколь угодно малым непрерывным видоизменением (к чему и сводится его e-сдвиг) превращен в полиэдр той же, но не меньшей, размерности. Эта теорема так же, как и определение размерности dim Xдля компактов, может быть переформулирована в чисто топологич. терминах, причем снова "сколь угодно малые" числа e>0 заменяются "сколь угодно мелкими" покрытиями w. Это позволяет аналогичную теорему сформулировать для любых нормальных пространств и придти к заключению, что в некром (все же наглядном) геометрическом смысле всякое n-мерное нормальное пространство "похоже" и даже "сколь угодно мало отличается" от n-мерного полиэдра. - прообраз сферы Sn-1 при этом отображении, Ф =f-1Sn-1. Отображение
- прообраз сферы Sn-1 при этом отображении, Ф =f-1Sn-1. Отображение  наз. существенным, если всякое непрерывное отображение
наз. существенным, если всякое непрерывное отображение 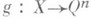 , совпадающее с f во всех точках
, совпадающее с f во всех точках  , есть отображение на весь шар Q". Упомянутая теорема Александрова утверждает, что нормальное пространство Xтогда и только тогда имеет размерность dim
, есть отображение на весь шар Q". Упомянутая теорема Александрова утверждает, что нормальное пространство Xтогда и только тогда имеет размерность dim  , когда пространство Xможно существенно отобразить на n-мерный шар. Из этой теоремы выводится теорема суммы (доказанная для компактов П. С. Урысоном и К. Менгером еще в самом начале развития Р. т.): если (нормальное) пространство Xразмерности dim Х=п является объединением конечного или счетного числа своих замкнутых множеств
, когда пространство Xможно существенно отобразить на n-мерный шар. Из этой теоремы выводится теорема суммы (доказанная для компактов П. С. Урысоном и К. Менгером еще в самом начале развития Р. т.): если (нормальное) пространство Xразмерности dim Х=п является объединением конечного или счетного числа своих замкнутых множеств  , то по крайней мере для одного из этих
, то по крайней мере для одного из этих  имеет место
имеет место 
 , к-рая наз. группой коэффициентов. Тогда можно говорить о циклах компакта Xно этой группе коэффициентов, об их носителях
, к-рая наз. группой коэффициентов. Тогда можно говорить о циклах компакта Xно этой группе коэффициентов, об их носителях  и, в частности, о циклах, гомологичных нулю в Xпо области коэффициентов
и, в частности, о циклах, гомологичных нулю в Xпо области коэффициентов  , причем эти понятия можно эквивалентным образом понимать как в смысле теории гомологии Александрова - Чеха, так и в смысле гомологич. теории Вьеториса.
, причем эти понятия можно эквивалентным образом понимать как в смысле теории гомологии Александрова - Чеха, так и в смысле гомологич. теории Вьеториса. как наибольшее целое число птакое, что в компакте Xимеется (n-1)-мерный цикл Zn-l, гомологичный нулю в X, но не гомологичный нулю на нек-ром своем носителе Ф. Оказывается, что dim Xесть гомологич. размерность по группе
как наибольшее целое число птакое, что в компакте Xимеется (n-1)-мерный цикл Zn-l, гомологичный нулю в X, но не гомологичный нулю на нек-ром своем носителе Ф. Оказывается, что dim Xесть гомологич. размерность по группе  , являющейся факторгруппой группы всех действительных чисел по подгруппе целых чисел, и она является наибольшей среди всех вообще гомологич. размерностей.
, являющейся факторгруппой группы всех действительных чисел по подгруппе целых чисел, и она является наибольшей среди всех вообще гомологич. размерностей. равна гомологич. размерности по бикомпактной группе
равна гомологич. размерности по бикомпактной группе 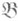 , двойственной группе
, двойственной группе  в смысле теории характеров Понтрягина. Отсюда следует, что размерность dim Xсовпадает с когомологической размерностью по группе целых чисел.
в смысле теории характеров Понтрягина. Отсюда следует, что размерность dim Xсовпадает с когомологической размерностью по группе целых чисел.