|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАЗЛИЧАЮЩАЯЗначение РАЗЛИЧАЮЩАЯ в математической энциклопедии: различающая кодепь,- препятствие к продолжению гомотопии между отображениями. Пусть X - нек-рое клеточное пространство, Y - односвязное топологич. пространство; пусть, далее, даны два отображения f, g: (где I=[0, 1] и Xn есть n-мерный остов пространства X).между ними на (n-1)-мерном остове. Для каждой ориентированной n-мерной клетки е п пространства Xограничение отображения Справедливы является коциклом; 3) класс когомологий тогда и только тогда равен нулю, когда между f и gимеется гомотопия на Xn, совпадающая с Fна Х n-2. Без ограничения общности можно считать, что f и gсовпадают на Xn-1 и что F(x, t)=f(x)=g(x).для 1) dn(f, g)=-dn(g, f), в частности dn(f, f)=0; 2) dn(f, g)+dn(g, h) =dn(f, h); 3) для любого отображения f : Пусть теперь заданы два отображения Таким образом, если gпродолжается на Х п + 1, то |
|
|
|

 . и гомотопия
. и гомотопия 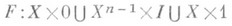
 задает отображение
задает отображение 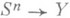 (Sn есть n-мерная сфера) и, значит, элемент группы pn(Y). Таким образом возникает коцепь
(Sn есть n-мерная сфера) и, значит, элемент группы pn(Y). Таким образом возникает коцепь  ) (более точным было бы обозначение
) (более точным было бы обозначение  ), к-рая и наз. различающей коцепью; коцепь dn(f, g).является препятствием к продолжению отображения Fна
), к-рая и наз. различающей коцепью; коцепь dn(f, g).является препятствием к продолжению отображения Fна  X
X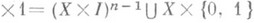 следующие утверждения: 1) dn(f, g)=0 тогда и только тогда, когда гомотопия между fи gпродолжается на Xn;2) коцепь
следующие утверждения: 1) dn(f, g)=0 тогда и только тогда, когда гомотопия между fи gпродолжается на Xn;2) коцепь 


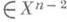 . При этих предположениях справедливы следующие утверждения:
. При этих предположениях справедливы следующие утверждения: и любой коцепи
и любой коцепи 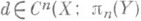 ) существует такое отображение g, что
) существует такое отображение g, что  и dn(f, g) = d.
и dn(f, g) = d. и пусть
и пусть  и - препятствия к продолжениям
и - препятствия к продолжениям  соответствующих
соответствующих  отображений. Роль Р. в теории препятствий определяется следующим предло 1 жением:
отображений. Роль Р. в теории препятствий определяется следующим предло 1 жением:
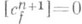 , а если
, а если  , то
, то 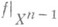 продолжается на Xn +1. Ю. Б. Рудяк.
продолжается на Xn +1. Ю. Б. Рудяк.