|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАДОНА ПРЕОБРАЗОВАНИЕЗначение РАДОНА ПРЕОБРАЗОВАНИЕ в математической энциклопедии: интегральное преобразование функций от нескольких переменных, родственное Фурье преобразованию. Введено И. Радоном (см. [1]). Пусть f(x1, . . ., х п) - непрерывная и достаточно быстро убывающая на бесконечности функция от действительных переменных Для любой гиперплоскости в И определяется интеграл где Vг - евклидовым (n-1)-мерный объем на гиперплоскости Г. Функция наз. преобразованием Радона функции f. Она является однородной функцией своих переменных степени -1: и связана с преобразованием Фурье С Р. п. непосредственным образом связана задача, восходящая к И. Радону, о восстановлении функции f по значениям ее интегралов, вычисленных по всем гиперплоскостям пространства Лит.:[1] Radon J., "Вег. Verh. Sachs. Acad.", 1917, Bd 69, S. 262-77; [2] Гельфанд И. М., Граев М. И., В и л е н к и н Н. Я., Интегральная геометрия ..., М., 1962. Р. А. Минлос. |
|
|
|

 , i=l, 2, ..., n, n=1, 2, ...
, i=l, 2, ..., n, n=1, 2, ...

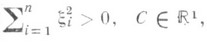


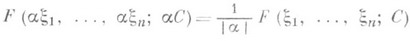
 ,
,  , функции f формулой
, функции f формулой 
 (т. <е. задача об обращении Р. п.).
(т. <е. задача об обращении Р. п.).