|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕЗначение РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ в математической энциклопедии: общее название Класса распределений вероятностей, возникающего при распространении идеи "равновозможности исходов" на непрерывный случай. Подобно нормальному распределению Р. р. появляется в теории вероятностей как точное распределение в одних задачах и как предельное - в других. Р. р. на отрезке числовой прямой (прямоугольное распределение). Р. р. на каком-либо отрезке [ а, b], а<b, - это распределений вероятностей, имеющее плотность Понятие Р. р. на [ а, b] соответствует представлению о случайном выборе точки на этом отрезке "наудачу". Математич. ожидание и дисперсия Р. р. равны, соответственно, (b+a)/2 и (b-а)2/12. Функция распределения задается формулой а характеристич. функция - формулой Случайную величину с Р. р. на [0,1] можно построить, исходя из последовательности независимых случайных величин Х 1, Х 2, . . ., принимающих значения 0 и 1 с вероятностями 1/2 полагая ( Х n являются цифрами в двоичном разложении X). Случайное число Xимеет Р. р. на отрезке [0,1]. Этот факт имеет важные статистич. приложения, см., напр., Случайные и псевдослучайные числа. Если независимые случайные величины Х 1 и Х 2 имеют Р. р. на [0,1], то их сумма Х 1+Х 2 имеет так наз. треугольное распределение на [0,2] с плотностью u2 (х)=1 -|1-х | для В общем случае сумма X1+X2+. . . +Х n независимых величин с Р. р. на [0,1] распределена с плотностью для Распределение суммы В статистич. приложениях процедура построения случайной величины с заданной функцией распределения F(х).основана на следующем факте. Пусть случайная величина Yраспределена равномерно на [0,1] и функция распределения F(х).непрерывна и строго возрастает. Тогда случайная величина P.p. на отрезке как предельное распределение. Ниже приводятся типичные примеры возникновения Р. р. на [0,1] в качестве предельного. 1) Пусть X1, X2, . . ., Х n,... - независимые случайные величины, имеющие одну и ту же непрерывную функцию распределения. Тогда распределение их суммы Sn, приведенной по mod 1, т. е., иными словами, распределение дробной части {Sn} суммы Sn, сходится к равномерному на [0, 1] распределению. 2) Пусть параметры 3) Р. р. встречается как предельное распределение дробных долей нек-рых функций g(n) натурального аргумента п. Напр., при иррациональном a. доля тех имеет пределом при Р. р. на под множествах где Собратна k-мерному объему (или лебеговой мере) области D. Рассматривают также и Р. р. на поверхностях. Так, "случайное направление" (напр., в Роль Р. р. на алгебраич. группах играет нормированная Хаара мера. Лит.:[1] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 2, М., 1967. А. В. Прохоров. |
|
|
|

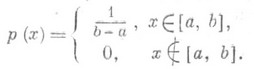
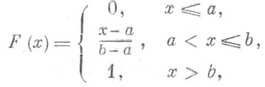
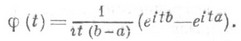
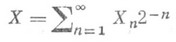
 и u2(x)=0 для
и u2(x)=0 для 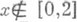 . Сумма трех независимых случайных величин с Р. р. на [0,1] имеет распределение на [0,3] с плотностью
. Сумма трех независимых случайных величин с Р. р. на [0,1] имеет распределение на [0,3] с плотностью 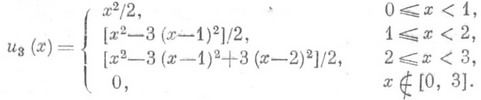
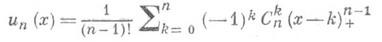
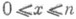 и и п (х)=0 для
и и п (х)=0 для  ; здесь
; здесь 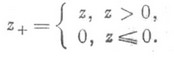
 нормированной математич. ожиданием n/2 и среднеквадратич. отклонением
нормированной математич. ожиданием n/2 и среднеквадратич. отклонением 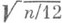 , с ростом пбыстро сближается с нормальным распределением с параметрами 0 и 1 (уже при n=3 приближение удовлетворительно для многих практич. целей).
, с ростом пбыстро сближается с нормальным распределением с параметрами 0 и 1 (уже при n=3 приближение удовлетворительно для многих практич. целей).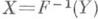 имеет функцию распределения F(х).(в общем случае надо заменить в определении Xфункцию F-1 (у).на нек-рый ее аналог, а именно
имеет функцию распределения F(х).(в общем случае надо заменить в определении Xфункцию F-1 (у).на нек-рый ее аналог, а именно 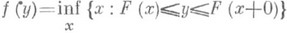 ).
).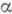 и
и 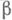 имеют абсолютно непрерывное совместное распределение; тогда при
имеют абсолютно непрерывное совместное распределение; тогда при  распределение
распределение 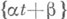 сходится к равномерному на [0,1].
сходится к равномерному на [0,1].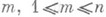 , из пдля к-рых
, из пдля к-рых 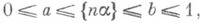
 величину b-а.
величину b-а. . Пример Р. р. в прямоугольнике встречается уже в Бюффона задаче (см. также Геометрические вероятности, Стохастическая геометрия]. Р. р. на нек-ром ограниченном множестве Dв евклидовом пространстве
. Пример Р. р. в прямоугольнике встречается уже в Бюффона задаче (см. также Геометрические вероятности, Стохастическая геометрия]. Р. р. на нек-ром ограниченном множестве Dв евклидовом пространстве  определяется как распределение, имеющее плотность
определяется как распределение, имеющее плотность 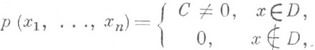
 ) определяют вектором, идущим из начала координат в случайную точку поверхиости единичной сферы, равномерно распределенную в том смысле, что вероятность ее попадания в какую-либо часть поверхности пропорциональна площади этой части.
) определяют вектором, идущим из начала координат в случайную точку поверхиости единичной сферы, равномерно распределенную в том смысле, что вероятность ее попадания в какую-либо часть поверхности пропорциональна площади этой части.