|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕССЕЛЯ ФУНКЦИИЗначение БЕССЕЛЯ ФУНКЦИИ в математической энциклопедии: - цилиндрические функции1-го рода. Б. ф. .индекса рможет быть определена рядом сходящемся на всей плоскости. Б. ф. индекса рявляется решением соответствующего Бесселя уравнения. При действительных положительных значениях аргумента и индекса ( Нули Б. ф. [корни уравнения Б. ф. В бесконечном промежутке его заменяет интеграл Фурье-Бесселя Важную роль в теории Б. ф. и их применений играют: 1) интегральное представление 2) производящая функция 3) теорема сложения для Б. ф. нулевого индекса 4) рекуррентные формулы Лит. ем. при статье Цилиндрические функции. П. И. Лизоркин. BETA-РАСПРЕДЕЛЕНИЕ - непрерывное сосредоточенное на (0, 1) распределение вероятностей с плотностью где параметры ( (эта функция табулирована, см. [1], [2] ). Моменты Б.-р. выражаются формулой в частности, математич. ожидание и дисперсия равны
При замене в (1) Это распределение наз. Б.-р. второго рода, в отличие от Б.-р. (1). Распределения (1) и (2) соответствуют распределениям "типа I" и "типа VI" в системе Пирсона кривых. Один из важных случаев возникновения Б.-р. таков: если (случайная величина (обычно значения F-распределения вычисляются с помощью таблиц Б.-р.). Функция Б.-р. позволяет также вычислять значения функций биномиального распределения, ввиду соотношения Б.-р. находит применение не только в математич. статистике, так, напр., плотность Б.-р. является весовой функцией для системы ортогональных Якоби многочленов. Лит.:[1] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2изд., М., 1968; |2] Пирсон К. Таблицы неполной бета-функции, пер. с англ., М., 1974. А. В. Прохоров. BETA-ФУНКЦИЯ, В-функция, В-функция Эйлера, эйлеров интеграл 1-го рода - функция двух переменных Значения Б.-ф. при различных значениях параметров Справедлива формула В случае комплексных ри q интеграл (*) сходится, когда
В. И. Битюцков. |
|
|
|



 - действительное число) Б. ф. действительна, график ее имеет вид затухающего колебания (см. рис.); при четном индексе Б. ф. четна, при нечетном - нечетна. Поведение Б. ф. в окрестности нуля дается первыми слагаемыми ряда (*); при больших хсправедливо асимптотич. представление
- действительное число) Б. ф. действительна, график ее имеет вид затухающего колебания (см. рис.); при четном индексе Б. ф. четна, при нечетном - нечетна. Поведение Б. ф. в окрестности нуля дается первыми слагаемыми ряда (*); при больших хсправедливо асимптотич. представление 
 ] - простые, при этом нули
] - простые, при этом нули  лежат между нулями
лежат между нулями  . Б. ф. "полуцелого" порядка
. Б. ф. "полуцелого" порядка  выражаются через тригонометрич. функции; в частности,
выражаются через тригонометрич. функции; в частности,
 - положительные нули
- положительные нули  образуют ортогональную с весом хв промежутке
образуют ортогональную с весом хв промежутке  систему. При определенных условиях имеет место разложение
систему. При определенных условиях имеет место разложение 






 неотрицательны и нормирующий множитель
неотрицательны и нормирующий множитель  есть бета-функция Эйлера
есть бета-функция Эйлера 
 - гамма-функция). Функция распределения выражается через неполную бета-функцию
- гамма-функция). Функция распределения выражается через неполную бета-функцию 

 и
и  соответственно. Если
соответственно. Если  то кривая плотности
то кривая плотности  имеет единственную точку максимума
имеет единственную точку максимума  и обращается в нуль на концах интервала. Если
и обращается в нуль на концах интервала. Если  или
или  , то одна из крайних ординат графика бесконечна, а если и
, то одна из крайних ординат графика бесконечна, а если и  , и
, и 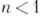 , то обе ординаты на концах интервала бесконечны и кривая имеет
, то обе ординаты на концах интервала бесконечны и кривая имеет  -образную форму. При
-образную форму. При  Б.-р. превращается в равномерное распределение в интервале
Б.-р. превращается в равномерное распределение в интервале 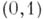 . Другим частным случаем Б.-р. является так наз. арксинуса распределение
. Другим частным случаем Б.-р. является так наз. арксинуса распределение
 получается распределение с плотностью
получается распределение с плотностью 
 независимы и имеют гамма-распределения с параметрами тип соответственно, то случайная величина
независимы и имеют гамма-распределения с параметрами тип соответственно, то случайная величина  имеет Б.-р. с плотностью
имеет Б.-р. с плотностью 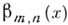 . Этот факт в большой степени объясняет ту роль, к-рую Б.-р. играет в приложениях, в частности в математич. статистике: распределения многих важнейших статистик сводятся к Б.-р. Напр., функция распределения F-отношения
. Этот факт в большой степени объясняет ту роль, к-рую Б.-р. играет в приложениях, в частности в математич. статистике: распределения многих важнейших статистик сводятся к Б.-р. Напр., функция распределения F-отношения 
 имеет
имеет  -распределение с kстепенями свободы) выражается формулой
-распределение с kстепенями свободы) выражается формулой 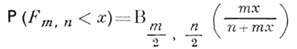

 , определяемая при
, определяемая при  равенством
равенством 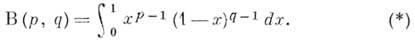
 связаны между собой следующими соотношениями
связаны между собой следующими соотношениями 

 Б.-ф. выражается через гамма-функцию:
Б.-ф. выражается через гамма-функцию: