|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕССЕЛЕВ ПОТЕНЦИАЛЗначение БЕССЕЛЕВ ПОТЕНЦИАЛ в математической энциклопедии: потенциал вида где Основные свойства бесселевых ядер но, в отличие от потенциалов Рисса, Б. <п. применимы при всех при Если и
где Лит.:[1] Ни Кольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969, гл. 8: [2] Aronszajn N., Smith К. Т., "Ann. Inst. Fourier", 1961, v. 11, p. 385 - 475. E. Д. Соломениев. |
|
|
|


 - точки евклидова пространства
- точки евклидова пространства  - борелевская мера на
- борелевская мера на 

 - модифицированная цилиндрическая функция (или бесселева функция) 2-го рода порядка
- модифицированная цилиндрическая функция (или бесселева функция) 2-го рода порядка  , или функция Макдональда порядка
, или функция Макдональда порядка  ;
; наз. бесселевым ядром.
наз. бесселевым ядром. те же, что ядер Рисса (см. Рисса потенциал):положительность, непрерывность при
те же, что ядер Рисса (см. Рисса потенциал):положительность, непрерывность при  , свойство композиции
, свойство композиции 
 , поскольку
, поскольку 

 - натуральное число, мера
- натуральное число, мера  абсолютно непрерывна с интегрируемой в квадрате плотностью
абсолютно непрерывна с интегрируемой в квадрате плотностью  то для Б. п. выполняются тождества
то для Б. п. выполняются тождества 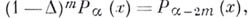

 - Лапласа оператор в
- Лапласа оператор в  . Иначе говоря, функция
. Иначе говоря, функция  есть фундаментальное решение оператора
есть фундаментальное решение оператора  .
.