"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕСКОНЕЧНОСТЬ
Значение БЕСКОНЕЧНОСТЬ в математической энциклопедии:
- понятие, возникающее в различных разделах математики в основном как противопоставление понятию конечного. Понятие Б. используется в аналитич. и геометрич. теориях для обозначения "несобственных" или "бесконечно удаленных" элементов, в теории множеств и математич. логике при изучении "бесконечных множеств" и в др. разделах математики.
1) Представление о бесконечно малых и бесконечно больших переменных величинах является одним из основных в математич. анализе. Предшествовавшая современному подходу к понятию бесконечно малой концепция, по к-рой конечные величины составлялись из бесконечно большого числа бесконечно малых "неделимых" (см. "Неделимых" метод), трактовавшихся не как переменные, а как постоянные и меньшие любой конечной величины, может служить одним из примеров незаконного отрыва бесконечного от конечного: реальный смысл имеет только разложение конечных величин на неограниченно возрастающее число неограниченно убывающих слагаемых.
2) Совсем в другой логич. обстановке Б. появляется в математике в виде "несобственных" бесконечно удаленных геометрич. образов (см. Бесконечно удаленные элементы). Здесь, напр., бесконечно удаленная точка на прямой арассматривается как -особый постоянный объект, "присоединенный" к обычным конечным точкам. Однако неразрывная связь бесконечного с конечным обнаруживается и здесь, хотя бы при проектировании из центра, лежащего вне прямой, при к-ром бесконечно удаленной точке оказывается соответствующей прямая, проходящая через центр проектирования и параллельная основной прямой а.
Аналогичный характер имеет пополнение системы действительных чисел двумя "несобственными" числами  , соответствующее многим запросам анализа и теории функций действительного переменного. Можно подойти с такой же точки зрения и к пополнению ряда натуральных чисел
, соответствующее многим запросам анализа и теории функций действительного переменного. Можно подойти с такой же точки зрения и к пополнению ряда натуральных чисел  трансфинитными числами
трансфинитными числами  В связи с различием между переменными бесконечно малыми и бесконечно большими величинами, с одной стороны, и "несобственными" бесконечно большими числами, рассматриваемыми как постоянные, - с другой, возникли термины "потенциальная" Б. (для первых) и "актуальная" Б. (для вторых). В этом первоначальном понимании (о другом, современном понимании, см. ниже) спор между сторонниками потенциальной и актуальной Б. можно считать законченным. Бесконечно малые и бесконечно большие, лежащие в основе определения производной (как отношения бесконечно малых) и интеграла(как суммы бесконечно большого числа бесконечно малых) и примыкающих сюда концепций математич. анализа, должны восприниматься как "потенциальные". Наряду с этим в надлежащей логич. обстановке в математику вполне закономерно входят и "актуальные" бесконечно большие "несобственные" числа (и даже во многих различных аспектах: как количественные и порядковые трансфинитные числа в теории множеств, как несобственные элементы
В связи с различием между переменными бесконечно малыми и бесконечно большими величинами, с одной стороны, и "несобственными" бесконечно большими числами, рассматриваемыми как постоянные, - с другой, возникли термины "потенциальная" Б. (для первых) и "актуальная" Б. (для вторых). В этом первоначальном понимании (о другом, современном понимании, см. ниже) спор между сторонниками потенциальной и актуальной Б. можно считать законченным. Бесконечно малые и бесконечно большие, лежащие в основе определения производной (как отношения бесконечно малых) и интеграла(как суммы бесконечно большого числа бесконечно малых) и примыкающих сюда концепций математич. анализа, должны восприниматься как "потенциальные". Наряду с этим в надлежащей логич. обстановке в математику вполне закономерно входят и "актуальные" бесконечно большие "несобственные" числа (и даже во многих различных аспектах: как количественные и порядковые трансфинитные числа в теории множеств, как несобственные элементы  системы действительных чисел и т. д.).
системы действительных чисел и т. д.).
В математике приходится иметь дело с двумя способами присоединения к числовой системе бесконечных "несобственных" элементов.
а) С проективной точки зрения на прямой находится одна "бесконечно удаленная точка". В обычной метрич. системе координат этой точке естественно приписать абсциссу  . Такое же присоединение к числовой системе одной Б. без знака употребляется в теории функций комплексного переменного. В элементарном анализе при изучении рациональных функций
. Такое же присоединение к числовой системе одной Б. без знака употребляется в теории функций комплексного переменного. В элементарном анализе при изучении рациональных функций 
 , где
, где  - многочлены, в тех точках, где
- многочлены, в тех точках, где  имеет нуль более высокого порядка, чем
имеет нуль более высокого порядка, чем  , естественно положить
, естественно положить  .
.
Для несобственного элемента  устанавливаются такие правила действий:
устанавливаются такие правила действий:

Неравенства с участием 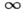 не рассматриваются: бессмысленно спрашивать, больше или меньше
не рассматриваются: бессмысленно спрашивать, больше или меньше  , чем конечное а.
, чем конечное а.
б) При изучении действительных функций действительного переменного систему действительных чисел дополняют двумя несобственными элементами  и
и 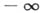 . Тогда можно положить, что
. Тогда можно положить, что  для любого конечного а, и сохранить основные свойства неравенств в расширенной числовой системе. Для
для любого конечного а, и сохранить основные свойства неравенств в расширенной числовой системе. Для  и
и  устанавливаются такие правила действий:
устанавливаются такие правила действий:

3) Основной интерес, но и основные трудности математич. учения о Б. сосредоточиваются на вопросе о природе бесконечных множеств математич. объектов. Следует, в частности, иметь в виду, что достигнутая ныне полная отвлеченность и законченность теории бесконечно больших и бесконечно малых переменных величин заключается лишь в сведении всех трудностей этой теории к вопросу обоснования учения о числе, в к-рое существенно входит представление о Б. системы чисел. Утверждение о том, что убесконечно мало, имеет смысл только при указании характера изменения ув зависимости от к.-л. другого переменного х напр., говорят, что убесконечно мало при  , если при любом
, если при любом  существует такое
существует такое  , что из
, что из  вытекает
вытекает  . В самое это определение уже входит предположение, что функция
. В самое это определение уже входит предположение, что функция  определена для бесконечного множества значений х(напр., для всех действительных х, достаточно близких к а). В теории множеств терминам "актуальная" и "потенциальная" Б. придают обычно глубокий смысл, не имеющий ничего общего с наименованием каждой бесконечной мощности "актуально бесконечным числом". Дело в том, что бесконечные системы математич. объектов (напр., натуральных или действительных чисел) никогда не задаются простым перечислением, как это возможно для конечных систем объектов. Было бы очевидным абсурдом предполагать, что кто-либо "образовал" множество натуральных чисел, перечислив их фактически "все" одно за другим. На самом деле множество натуральных чисел изучают, исходя из процесса образования его элементов переходом от n к п+1. В случае континуума действительных чисел уже рассмотрение одного его элемента - действительного числа - приводит к изучению процесса образования его последовательных приближенных значений, а рассмотрение всего множества действительных чисел приводит к изучению общих свойств такого рода процессов образования его элементов. В этом именно смысле сама Б. натурального ряда, или системы всех действительных чисел (континуума), может характеризоваться как Б. лишь "по-тенциаль'ная". Точке зрения потенциальной Б. противополагается взгляд на бесконечные множества как "актуально" заданные, независимо от процесса их образования. Выяснение вопроса о том, в какой мере и при каких условиях при изучении бесконечных множеств законно такое абстрагирование от процесса их образования, еще нельзя считать законченным. См. также Абстракция актуальной бесконечности, Абстракция потенциальной осуществимости. А. <Н. <Колмогоров.
определена для бесконечного множества значений х(напр., для всех действительных х, достаточно близких к а). В теории множеств терминам "актуальная" и "потенциальная" Б. придают обычно глубокий смысл, не имеющий ничего общего с наименованием каждой бесконечной мощности "актуально бесконечным числом". Дело в том, что бесконечные системы математич. объектов (напр., натуральных или действительных чисел) никогда не задаются простым перечислением, как это возможно для конечных систем объектов. Было бы очевидным абсурдом предполагать, что кто-либо "образовал" множество натуральных чисел, перечислив их фактически "все" одно за другим. На самом деле множество натуральных чисел изучают, исходя из процесса образования его элементов переходом от n к п+1. В случае континуума действительных чисел уже рассмотрение одного его элемента - действительного числа - приводит к изучению процесса образования его последовательных приближенных значений, а рассмотрение всего множества действительных чисел приводит к изучению общих свойств такого рода процессов образования его элементов. В этом именно смысле сама Б. натурального ряда, или системы всех действительных чисел (континуума), может характеризоваться как Б. лишь "по-тенциаль'ная". Точке зрения потенциальной Б. противополагается взгляд на бесконечные множества как "актуально" заданные, независимо от процесса их образования. Выяснение вопроса о том, в какой мере и при каких условиях при изучении бесконечных множеств законно такое абстрагирование от процесса их образования, еще нельзя считать законченным. См. также Абстракция актуальной бесконечности, Абстракция потенциальной осуществимости. А. <Н. <Колмогоров.

 , соответствующее многим запросам анализа и теории функций действительного переменного. Можно подойти с такой же точки зрения и к пополнению ряда натуральных чисел
, соответствующее многим запросам анализа и теории функций действительного переменного. Можно подойти с такой же точки зрения и к пополнению ряда натуральных чисел  трансфинитными числами
трансфинитными числами  В связи с различием между переменными бесконечно малыми и бесконечно большими величинами, с одной стороны, и "несобственными" бесконечно большими числами, рассматриваемыми как постоянные, - с другой, возникли термины "потенциальная" Б. (для первых) и "актуальная" Б. (для вторых). В этом первоначальном понимании (о другом, современном понимании, см. ниже) спор между сторонниками потенциальной и актуальной Б. можно считать законченным. Бесконечно малые и бесконечно большие, лежащие в основе определения производной (как отношения бесконечно малых) и интеграла(как суммы бесконечно большого числа бесконечно малых) и примыкающих сюда концепций математич. анализа, должны восприниматься как "потенциальные". Наряду с этим в надлежащей логич. обстановке в математику вполне закономерно входят и "актуальные" бесконечно большие "несобственные" числа (и даже во многих различных аспектах: как количественные и порядковые трансфинитные числа в теории множеств, как несобственные элементы
В связи с различием между переменными бесконечно малыми и бесконечно большими величинами, с одной стороны, и "несобственными" бесконечно большими числами, рассматриваемыми как постоянные, - с другой, возникли термины "потенциальная" Б. (для первых) и "актуальная" Б. (для вторых). В этом первоначальном понимании (о другом, современном понимании, см. ниже) спор между сторонниками потенциальной и актуальной Б. можно считать законченным. Бесконечно малые и бесконечно большие, лежащие в основе определения производной (как отношения бесконечно малых) и интеграла(как суммы бесконечно большого числа бесконечно малых) и примыкающих сюда концепций математич. анализа, должны восприниматься как "потенциальные". Наряду с этим в надлежащей логич. обстановке в математику вполне закономерно входят и "актуальные" бесконечно большие "несобственные" числа (и даже во многих различных аспектах: как количественные и порядковые трансфинитные числа в теории множеств, как несобственные элементы  системы действительных чисел и т. д.).
системы действительных чисел и т. д.). . Такое же присоединение к числовой системе одной Б. без знака употребляется в теории функций комплексного переменного. В элементарном анализе при изучении рациональных функций
. Такое же присоединение к числовой системе одной Б. без знака употребляется в теории функций комплексного переменного. В элементарном анализе при изучении рациональных функций 
 , где
, где  - многочлены, в тех точках, где
- многочлены, в тех точках, где  имеет нуль более высокого порядка, чем
имеет нуль более высокого порядка, чем  , естественно положить
, естественно положить  .
. устанавливаются такие правила действий:
устанавливаются такие правила действий:
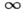 не рассматриваются: бессмысленно спрашивать, больше или меньше
не рассматриваются: бессмысленно спрашивать, больше или меньше  , чем конечное а.
, чем конечное а. и
и 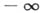 . Тогда можно положить, что
. Тогда можно положить, что  для любого конечного а, и сохранить основные свойства неравенств в расширенной числовой системе. Для
для любого конечного а, и сохранить основные свойства неравенств в расширенной числовой системе. Для  и
и  устанавливаются такие правила действий:
устанавливаются такие правила действий:
 , если при любом
, если при любом  существует такое
существует такое  , что из
, что из  вытекает
вытекает  . В самое это определение уже входит предположение, что функция
. В самое это определение уже входит предположение, что функция  определена для бесконечного множества значений х(напр., для всех действительных х, достаточно близких к а). В теории множеств терминам "актуальная" и "потенциальная" Б. придают обычно глубокий смысл, не имеющий ничего общего с наименованием каждой бесконечной мощности "актуально бесконечным числом". Дело в том, что бесконечные системы математич. объектов (напр., натуральных или действительных чисел) никогда не задаются простым перечислением, как это возможно для конечных систем объектов. Было бы очевидным абсурдом предполагать, что кто-либо "образовал" множество натуральных чисел, перечислив их фактически "все" одно за другим. На самом деле множество натуральных чисел изучают, исходя из процесса образования его элементов переходом от n к п+1. В случае континуума действительных чисел уже рассмотрение одного его элемента - действительного числа - приводит к изучению процесса образования его последовательных приближенных значений, а рассмотрение всего множества действительных чисел приводит к изучению общих свойств такого рода процессов образования его элементов. В этом именно смысле сама Б. натурального ряда, или системы всех действительных чисел (континуума), может характеризоваться как Б. лишь "по-тенциаль'ная". Точке зрения потенциальной Б. противополагается взгляд на бесконечные множества как "актуально" заданные, независимо от процесса их образования. Выяснение вопроса о том, в какой мере и при каких условиях при изучении бесконечных множеств законно такое абстрагирование от процесса их образования, еще нельзя считать законченным. См. также Абстракция актуальной бесконечности, Абстракция потенциальной осуществимости. А. <Н. <Колмогоров.
определена для бесконечного множества значений х(напр., для всех действительных х, достаточно близких к а). В теории множеств терминам "актуальная" и "потенциальная" Б. придают обычно глубокий смысл, не имеющий ничего общего с наименованием каждой бесконечной мощности "актуально бесконечным числом". Дело в том, что бесконечные системы математич. объектов (напр., натуральных или действительных чисел) никогда не задаются простым перечислением, как это возможно для конечных систем объектов. Было бы очевидным абсурдом предполагать, что кто-либо "образовал" множество натуральных чисел, перечислив их фактически "все" одно за другим. На самом деле множество натуральных чисел изучают, исходя из процесса образования его элементов переходом от n к п+1. В случае континуума действительных чисел уже рассмотрение одного его элемента - действительного числа - приводит к изучению процесса образования его последовательных приближенных значений, а рассмотрение всего множества действительных чисел приводит к изучению общих свойств такого рода процессов образования его элементов. В этом именно смысле сама Б. натурального ряда, или системы всех действительных чисел (континуума), может характеризоваться как Б. лишь "по-тенциаль'ная". Точке зрения потенциальной Б. противополагается взгляд на бесконечные множества как "актуально" заданные, независимо от процесса их образования. Выяснение вопроса о том, в какой мере и при каких условиях при изучении бесконечных множеств законно такое абстрагирование от процесса их образования, еще нельзя считать законченным. См. также Абстракция актуальной бесконечности, Абстракция потенциальной осуществимости. А. <Н. <Колмогоров.