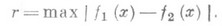ПРОСТРАНСТВО

Значение ПРОСТРАНСТВО в математической энциклопедии:

- логически мыслимая форма (или структура), служащая средой, в к-рой осуществляются другие формы и те или иные конструкции. Напр., в элементарной геометрии плоскость или пространство служат средой, где строятся разнообразные фигуры. В большинстве случаев в П. фиксируются отношения, сходные по формальным свойствам с обычными пространственными отношениями (расстояние между точками, равенство фигур и др.), так что о таких П. можно сказать, что они представляют логически мыслимые пространственно-подобные формы. Первым и важнейшим математич. П. является трехмерное евклидово пространство, представляющее приближенный абстрактный образ реального П. Общее понятие "П." в математике сложилось в результате обобщения и видоизменения понятий геометрии евклидова П. Первые П., отличные от трехмерного евклидова, были введены в 1-й пол. 19 в. Это были Лобачевского пространство и евклидово П. любого числа измерений (см. Многомерная геометрия). Общее понятие о математич. П. как "многократной протяженности" было выдвинуто в 1854 Б. Риманом (В. Riemann); оно обобщалось, уточнялось и конкретизировалось в разных направлениях: таковы, напр., риманово пространство, финслерово пространство, векторное пространство, гильбертово пространство, метрическое пространство, топологическое пространство. В современной математике П. определяют как множество каких-либо объектов, к-рые наз. его точками; ими могут быть геометрич. фигуры, функции, состояния физич. системы и т. д. Рассматривая их множество как П., отвлекаются от всяких их свойств и учитывают только те свойства их совокупности, к-рые определяются принятыми во внимание или введенными по определению отношениями. Эти отношения между точками и теми или иными фигурами, т. е. множествами точек, определяют "геометрию" П. При аксиоматич. ее построении основные свойства этих отношений выражаются в соответствующих аксиомах.

Примерами П. могут служить: 1) метрич. П., в к-рых определено расстояние между точками; напр., П. непрерывных функций на к.-л. отрезке [a, b], где точками служат функции f(x), непрерывные на [ а, b], а расстояние между f₁(x). и f₂(x) определяется как максимум модуля их разности:

2) "П. событий", играющее важную роль в геометрич. интерпретации теории относительности. Каждое событие характеризуется положением - координатами х, у, z и временем t, поэтому множество всевозможных событий оказывается четырехмерным П., где "точка" - событие определяется 4 координатами х, у, z, t.3) Фазовые П., рассматриваемые в теоретич. физике и механике. Фазовое П. физич. системы - это совокупность всех ее возможных состояний, к-рые рассматриваются при этом как точки этого П. А. <Д. Александров.