"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕСКОНЕЧНОГО ПОРЯДКА УРАВНЕНИЕ
Значение БЕСКОНЕЧНОГО ПОРЯДКА УРАВНЕНИЕ в математической энциклопедии:
в комплексной области - дифференциальное уравнение вида

где  - искомая функция комплексного переменного
- искомая функция комплексного переменного  - заданные .функции. Наиболее полно изучены .Б. п. у. с постоянными коэффициентами:
- заданные .функции. Наиболее полно изучены .Б. п. у. с постоянными коэффициентами:

Если .характеристич. функция

есть целая функция экспоненциального типа  , то левая часть
, то левая часть  имеет смысл при
имеет смысл при  , когда
, когда  - функция, аналитическая в круге
- функция, аналитическая в круге  . При
. При  необходимо предположить, что
необходимо предположить, что 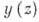 - целая функция. Отличие от уравнения конечного порядка состоит уже в том, что решение
- целая функция. Отличие от уравнения конечного порядка состоит уже в том, что решение  может иметь особенности, даже когда
может иметь особенности, даже когда  - целая функция. Если
- целая функция. Если  и
и  есть целая функция, то область существования любого решения выпукла [1]. Общее решение слагается из частного решения и общего решения соответствующего однородного уравнения. Пусть
есть целая функция, то область существования любого решения выпукла [1]. Общее решение слагается из частного решения и общего решения соответствующего однородного уравнения. Пусть  - корни характеристич. уравнения
- корни характеристич. уравнения  и
и  - соответственно их кратности. Однородное уравнение имеет элементарные частные решения
- соответственно их кратности. Однородное уравнение имеет элементарные частные решения 
 . Решению однородного уравнения можно отнести по определенному правилу ряд из элементарных решений. Если характеристич. функция
. Решению однородного уравнения можно отнести по определенному правилу ряд из элементарных решений. Если характеристич. функция  имеет правильный рост (в нек-ром определенном смысле), то найдется . подпоследовательность частичных сумм этого ряда, сходящаяся к
имеет правильный рост (в нек-ром определенном смысле), то найдется . подпоследовательность частичных сумм этого ряда, сходящаяся к  (см. [4]). В общем случае функцию
(см. [4]). В общем случае функцию  можно аппроксимировать с любой точностью конечными линейными комбинациями из элементарных решений [5]. В случае
можно аппроксимировать с любой точностью конечными линейными комбинациями из элементарных решений [5]. В случае  Б. п. у. может иметь неаналитические решения [2]. При нек-рых условиях эти решения образуют квазианалитический класс функций с менее сильными ограничениями на рост производных, чем в классич. теореме Данжуа - Карлемана.
Б. п. у. может иметь неаналитические решения [2]. При нек-рых условиях эти решения образуют квазианалитический класс функций с менее сильными ограничениями на рост производных, чем в классич. теореме Данжуа - Карлемана.
Б. п. у. имеют различные применения: для изучения последовательностей полиномов Дирихле, полноты систем аналитических функций, единственности аналитических и гармонических функций, разрешимости таких проблем анализа, как обобщенная проблема квазианалитичности, обобщенная проблема единственности моментов и т. д.
Лит.:[1] Ро1уa G., "Nachr. Ges. Wiss. Gottingen", 1927, S. 187-95; [2] Va1irоn G., "Ann. sclent. Ecole norm, super.", 1929, t. 46, № 1, p. 25-53; (3] Леонтьев А. Ф., "Тр. четвертого всесоюзн. матем. съезда", Л., 1964, т. 2, с. 648-60: [4] его же, "Матем. сб.", 1966, т. 70, № 1, с. 132-44; [5] Красичко в-Терновский И. Ф., "Матем. сб.", 1972, т. 88, № 3, с. 331 - 52. А. Ф. Леонтьев.


 - искомая функция комплексного переменного
- искомая функция комплексного переменного  - заданные .функции. Наиболее полно изучены .Б. п. у. с постоянными коэффициентами:
- заданные .функции. Наиболее полно изучены .Б. п. у. с постоянными коэффициентами:

 , то левая часть
, то левая часть  имеет смысл при
имеет смысл при  , когда
, когда  - функция, аналитическая в круге
- функция, аналитическая в круге  . При
. При  необходимо предположить, что
необходимо предположить, что 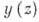 - целая функция. Отличие от уравнения конечного порядка состоит уже в том, что решение
- целая функция. Отличие от уравнения конечного порядка состоит уже в том, что решение  может иметь особенности, даже когда
может иметь особенности, даже когда  - целая функция. Если
- целая функция. Если  и
и  есть целая функция, то область существования любого решения выпукла [1]. Общее решение слагается из частного решения и общего решения соответствующего однородного уравнения. Пусть
есть целая функция, то область существования любого решения выпукла [1]. Общее решение слагается из частного решения и общего решения соответствующего однородного уравнения. Пусть  - корни характеристич. уравнения
- корни характеристич. уравнения  и
и  - соответственно их кратности. Однородное уравнение имеет элементарные частные решения
- соответственно их кратности. Однородное уравнение имеет элементарные частные решения 
 . Решению однородного уравнения можно отнести по определенному правилу ряд из элементарных решений. Если характеристич. функция
. Решению однородного уравнения можно отнести по определенному правилу ряд из элементарных решений. Если характеристич. функция  имеет правильный рост (в нек-ром определенном смысле), то найдется . подпоследовательность частичных сумм этого ряда, сходящаяся к
имеет правильный рост (в нек-ром определенном смысле), то найдется . подпоследовательность частичных сумм этого ряда, сходящаяся к  (см. [4]). В общем случае функцию
(см. [4]). В общем случае функцию  можно аппроксимировать с любой точностью конечными линейными комбинациями из элементарных решений [5]. В случае
можно аппроксимировать с любой точностью конечными линейными комбинациями из элементарных решений [5]. В случае  Б. п. у. может иметь неаналитические решения [2]. При нек-рых условиях эти решения образуют квазианалитический класс функций с менее сильными ограничениями на рост производных, чем в классич. теореме Данжуа - Карлемана.
Б. п. у. может иметь неаналитические решения [2]. При нек-рых условиях эти решения образуют квазианалитический класс функций с менее сильными ограничениями на рост производных, чем в классич. теореме Данжуа - Карлемана.