"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРОМЕЖУТОЧНЫЙ ЯКОБИАН
Значение ПРОМЕЖУТОЧНЫЙ ЯКОБИАН в математической энциклопедии:
набор комплексных торов, определяемых нечетномерными когомоло-гиями комплексного кэлерова многообразия, геометрия к-рых тесно связана с геометрией самого многообразия.
Пусть  (соответственно
(соответственно  ) - пространство re-мерных когомологий с действительными (соответственно с целыми) коэффициентами комилексно-аналитич. кэлерова многообразия X. На веществ. торе
) - пространство re-мерных когомологий с действительными (соответственно с целыми) коэффициентами комилексно-аналитич. кэлерова многообразия X. На веществ. торе

при нечетном пможно двумя различными способами ввести комплексную структуру, используя представление n-мерных когомологий с комплексными коэффициентами в виде прямой суммы 
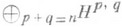 пространств Н р,q гармонич. форм типа ( р, q). Пусть
пространств Н р,q гармонич. форм типа ( р, q). Пусть 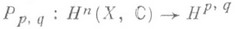 - проекция, а
- проекция, а
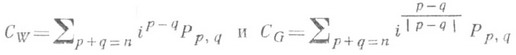
- операторы, переводящие когомологий с действительными коэффициентами в себя. Полагая

для любого w из  , получают комплексные структуры на Т п (Х), первая из к-рых
, получают комплексные структуры на Т п (Х), первая из к-рых  (X).наз. промежуточным якобианом Вейля, а вторая
(X).наз. промежуточным якобианом Вейля, а вторая  - промежуточным тором Гриффитса. Если X - многообразие Ходжа, то ходжева метрика на Xканонически определяет на П. я.
- промежуточным тором Гриффитса. Если X - многообразие Ходжа, то ходжева метрика на Xканонически определяет на П. я.  структуру поляризованного абелева многообразия, что не всегда имеет место для
структуру поляризованного абелева многообразия, что не всегда имеет место для  . С другой стороны, при голоморфной вариации многообразия Xпромежуточные торы
. С другой стороны, при голоморфной вариации многообразия Xпромежуточные торы 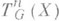 варьируются голоморфно [2], а П. я. Вейля этим свойством могут не обладать. Сup-произведение, задающее спаривание пространств
варьируются голоморфно [2], а П. я. Вейля этим свойством могут не обладать. Сup-произведение, задающее спаривание пространств  и
и  , где
, где  , определяет комплексное спаривание торов
, определяет комплексное спаривание торов  и
и  и двойственность между абелевыми многообразиями
и двойственность между абелевыми многообразиями  и
и  . В случае, когда
. В случае, когда  =2k+l, П. я.
=2k+l, П. я.  является самодвойственным абелевым многообразием с главной поляризацией, а
является самодвойственным абелевым многообразием с главной поляризацией, а  - главным тором. П. я. служит важным инвариантом кэлеровых многообразий. Если для двух многообразий Xи Yиз совпадения
- главным тором. П. я. служит важным инвариантом кэлеровых многообразий. Если для двух многообразий Xи Yиз совпадения  (соответственно
(соответственно 
 ) следует, что
) следует, что  , то говорят, что для Xвыполнена теорема Торелли. Теорема Торелли выполняется, напр., для алгебраич. кривых. С помощью П. я. была доказана нерациональность общей кубики в проективном пространстве Р 1 (см. [1]) и нек-рых других многообразий Фано.
, то говорят, что для Xвыполнена теорема Торелли. Теорема Торелли выполняется, напр., для алгебраич. кривых. С помощью П. я. была доказана нерациональность общей кубики в проективном пространстве Р 1 (см. [1]) и нек-рых других многообразий Фано.
Лит.:[1] Сlemens С.,Griffiths Ph., "Ann. Math.", 1972, v. 95, № 2, p. 281-356; [2] Сriffiths P h. "Amer. J. math.", 1968, v. 90, p. 568-626, 805-65; [3] Wei1 A., "Amer. J. math.", 1952, v. 74, p. 865 - 94. Вик. С. Куликов.

 (соответственно
(соответственно  ) - пространство re-мерных когомологий с действительными (соответственно с целыми) коэффициентами комилексно-аналитич. кэлерова многообразия X. На веществ. торе
) - пространство re-мерных когомологий с действительными (соответственно с целыми) коэффициентами комилексно-аналитич. кэлерова многообразия X. На веществ. торе 

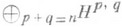 пространств Н р,q гармонич. форм типа ( р, q). Пусть
пространств Н р,q гармонич. форм типа ( р, q). Пусть 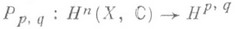 - проекция, а
- проекция, а 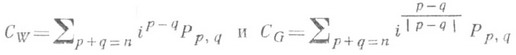

 , получают комплексные структуры на Т п (Х), первая из к-рых
, получают комплексные структуры на Т п (Х), первая из к-рых  (X).наз. промежуточным якобианом Вейля, а вторая
(X).наз. промежуточным якобианом Вейля, а вторая  - промежуточным тором Гриффитса. Если X - многообразие Ходжа, то ходжева метрика на Xканонически определяет на П. я.
- промежуточным тором Гриффитса. Если X - многообразие Ходжа, то ходжева метрика на Xканонически определяет на П. я.  структуру поляризованного абелева многообразия, что не всегда имеет место для
структуру поляризованного абелева многообразия, что не всегда имеет место для  . С другой стороны, при голоморфной вариации многообразия Xпромежуточные торы
. С другой стороны, при голоморфной вариации многообразия Xпромежуточные торы 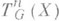 варьируются голоморфно [2], а П. я. Вейля этим свойством могут не обладать. Сup-произведение, задающее спаривание пространств
варьируются голоморфно [2], а П. я. Вейля этим свойством могут не обладать. Сup-произведение, задающее спаривание пространств  и
и  , где
, где  , определяет комплексное спаривание торов
, определяет комплексное спаривание торов  и
и  и двойственность между абелевыми многообразиями
и двойственность между абелевыми многообразиями  и
и  . В случае, когда
. В случае, когда  =2k+l, П. я.
=2k+l, П. я.  является самодвойственным абелевым многообразием с главной поляризацией, а
является самодвойственным абелевым многообразием с главной поляризацией, а  - главным тором. П. я. служит важным инвариантом кэлеровых многообразий. Если для двух многообразий Xи Yиз совпадения
- главным тором. П. я. служит важным инвариантом кэлеровых многообразий. Если для двух многообразий Xи Yиз совпадения  (соответственно
(соответственно 
 ) следует, что
) следует, что  , то говорят, что для Xвыполнена теорема Торелли. Теорема Торелли выполняется, напр., для алгебраич. кривых. С помощью П. я. была доказана нерациональность общей кубики в проективном пространстве Р 1 (см. [1]) и нек-рых других многообразий Фано.
, то говорят, что для Xвыполнена теорема Торелли. Теорема Торелли выполняется, напр., для алгебраич. кривых. С помощью П. я. была доказана нерациональность общей кубики в проективном пространстве Р 1 (см. [1]) и нек-рых других многообразий Фано.