" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ПРОИЗВОДНЫЙ ФУНКТОР

Значение ПРОИЗВОДНЫЙ ФУНКТОР в математической энциклопедии:

- функтор, "измеряющий" отклонение основного функтора от точного. Пусть Т( А, С).- аддитивный функтор из категории R₁ -модулей и R₂ -модулей в категорию R-модулей, ковариантный по первому аргументу и контравариантный по второму. Для инъективной резольвенты Xмодуля Аи проективной резольвенты Yмодуля Сполучают дважды градуированный комплекс Т( Х, Y). Группы гомологии ассоциированного одинарного комплекса Т( А, С).не зависят от выбора резольвент, обладают функторньтми свойствами и наз. правыми производными функторами RⁿT(A , С).функтора Т( А, С). Основное свойство П. ф.- существование бесконечных точных последовательностей

индуцированных короткими точными последовательностями

Левые П. ф. определяются двойственным образом. П. ф. функтора Нот обозначаются . Функтор 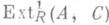классифицирует все расширения модуля А с ядром Сс точностью до эквивалентности (см. Бэра умножение, Когомологии алгебр).

Лит.:[1] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960; [2] Маклейн О., Гомология, пер. с англ., М., 1966. В. Е. Говоров.