|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРОЕКТИВНОЕ ПРОСТРАНСТВОЗначение ПРОЕКТИВНОЕ ПРОСТРАНСТВО в математической энциклопедии: совокупность всех подпространств инцидентностной структуры p-= 1) для любых двух различных точек ри qсуществует единственная прямая Lтакая, что pIL, qIL; 2) каждая прямая инцидентна по крайней мере с тремя точками; 3) если две различные прямые L, M пересекаются в точке ри выполнено qIL и rIL,a sIM, tIM, то прямые, проходящие через пары точек r, t и s, q, пересекаются. Подпространство Sпорождено множеством sточек из В П. н. определены операции сложения и пересечения подпространств. Суммой Р m+Р k подпространств Р m и Pk наз. наименьшее из подпространств, содержащее и Р m, и Pk. Пересечением Р m и Р k наз. наибольшее из подпространств, содержащееся и в Р m, и в Pk. Размерности подпространств Р m, Р k, их суммы и пересечения связаны соотношением Для любого Р m существует Pn-m-1 такое, что Р т для любого Pk (дедекиндово правило), т. е. относительно введенных операций П. п. является дедекиндовой решеткой с дополнениями. П. п. размерности больше двух дезаргово (см. Дезарга предложение), а следовательно, изоморфно П. п. (левому или правому) над подходящим телом k (см. [1]). Конечное тело необходимо коммутативно, следовательно, конечное П. п. размерности больше двух и порядка qизоморфно П. п. над Галуа полем PG(n, q). Конечное П. п. Р( п, q).содержит (q п+1-1)/(q-1) точек и Коллинеацией П. п. является перестановка ее точек, к-рая отображает прямые в прямые, при этом подпространства отображаются на подпространства. Нетривиальная коллинеация П. п. имеет не более одного центра и не более одной оси. Группа коллинеа-ций конечного П. п. PG(n, ph).имеет порядок, равный Каждое П. п. PG(n, q).допускает циклическую транзитивную группу коллинеаций (см. [3]). Корреляцией d П. <п. является перестановка подпространств, к-рая меняет включения, т. е. если Лит.:[1] Артин Э., Геометрическая алгебра, пер. с англ., М., 1969; [2] Ходж В., Пидо Д., Методы алгебраической геометрии, пер. с англ., т. 1, М., 1954; [3) Dеmbоwski P., Finite geometries, В. -[а. о.], 1968; [4] Segre В., Lectures on modern geometry, Roma, 1961. В. В. Афанасьев. |
|
|
|

 , где элементы множества
, где элементы множества  наз. точками, а элементы множества
наз. точками, а элементы множества  - прямыми, I - отношение инцидентности. Подпространством инцидентностной структуры p наз. подмножество S множества
- прямыми, I - отношение инцидентности. Подпространством инцидентностной структуры p наз. подмножество S множества  , для к-рого справедливо условие: если
, для к-рого справедливо условие: если  , то Множество точек прямой, проходящей через точки ри q, также принадлежат S. Инцидентностная структура p удовлетворяет следующим требованиям:
, то Множество точек прямой, проходящей через точки ри q, также принадлежат S. Инцидентностная структура p удовлетворяет следующим требованиям: (пишут S=<s>), если Sявляется пересечением всех подпространств, содержащих s. Множество точек s наз. независимым, если для любого
(пишут S=<s>), если Sявляется пересечением всех подпространств, содержащих s. Множество точек s наз. независимым, если для любого  имеет место
имеет место  . Упорядоченное максимальное и независимое множество точек подпространства Sназ. базисом S, а число его элементов d(S) - размерностью подпространства S. Подпространство размерности 0 является точкой, размерности 1 - проективной прямой. Подпространство размерности 2 наз. проективной плоскостью.
. Упорядоченное максимальное и независимое множество точек подпространства Sназ. базисом S, а число его элементов d(S) - размерностью подпространства S. Подпространство размерности 0 является точкой, размерности 1 - проективной прямой. Подпространство размерности 2 наз. проективной плоскостью. подпространств
подпространств 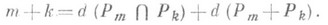
 Pn-m-1=P-1=
Pn-m-1=P-1= И Pm +Pn-m-1= Pn (Pn-m-1- дополнение Р т в Pn), и если Р т
И Pm +Pn-m-1= Pn (Pn-m-1- дополнение Р т в Pn), и если Р т Р r, то
Р r, то 
 (напр., левое) размерности пнад телом k - совокупность линейных подпространств нек-рого (n+1 )-мерного левого линейного пространства
(напр., левое) размерности пнад телом k - совокупность линейных подпространств нек-рого (n+1 )-мерного левого линейного пространства  над телом k;точками
над телом k;точками  являются прямые
являются прямые  , т. е. множества классов эквивалентности слева строк ( х 0, x1, . . ., х п), составленных из элементов тела kи не равных одновременно нулю (строки (x0, x1, . . ., х n).и (y0, y1, . . ., yn).эквивалентны слева, если существует такое
, т. е. множества классов эквивалентности слева строк ( х 0, x1, . . ., х п), составленных из элементов тела kи не равных одновременно нулю (строки (x0, x1, . . ., х n).и (y0, y1, . . ., yn).эквивалентны слева, если существует такое  , что xi=lyi, i=0, l, . . ., n); подпространствами
, что xi=lyi, i=0, l, . . ., n); подпространствами  являются (n+1 )-мерные подпространства
являются (n+1 )-мерные подпространства  . Можно установить нек-рое соответствие между левым
. Можно установить нек-рое соответствие между левым  и правым
и правым  П. п., при к-ром подпространству
П. п., при к-ром подпространству  соответствует
соответствует  (подпространства
(подпространства  и
и  наз. дуальными друг другу), пересечению подпространств соответствует сумма, а сумме - пересечение. Если нек-рое утверждение, основанное только на свойствах линейных подпространств, их пересечений и сумм, справедливо для
наз. дуальными друг другу), пересечению подпространств соответствует сумма, а сумме - пересечение. Если нек-рое утверждение, основанное только на свойствах линейных подпространств, их пересечений и сумм, справедливо для  , то справедливо и соответствующее утверждение для
, то справедливо и соответствующее утверждение для  . Это соответствие между свойствами пространств
. Это соответствие между свойствами пространств  и
и 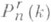 наз. принципом двойственности для П. п. (см. |2]).
наз. принципом двойственности для П. п. (см. |2]). подпространств размерности r(см. [4]).
подпространств размерности r(см. [4]).
 , то
, то  . П. п. допускает корреляцию, только если оно конечномерно. Важное значение в проективной геометрии играет корреляция порядка два, наз. поляритетом.
. П. п. допускает корреляцию, только если оно конечномерно. Важное значение в проективной геометрии играет корреляция порядка два, наз. поляритетом.