"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯЗначение БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯ в математической энциклопедии:
функция переменного х, к-рая при данном процессе изменения хстановится и остается по абсолютной величине меньше любого заданного числа. Точнее, функция  , определенная в окрестности точки х 0, наз. бесконечно малой функцией при х, стремящемся к х 0 , если для любого числа , определенная в окрестности точки х 0, наз. бесконечно малой функцией при х, стремящемся к х 0 , если для любого числа  найдется такое число найдется такое число  , что для всех , что для всех  , удовлетворяющих условию , удовлетворяющих условию  , выполняется , выполняется  . Этот факт записывается так: . Этот факт записывается так:

Символ 
напр., означает, что для любого  найдется такое найдется такое  что Для всех что Для всех  выполняется неравенство выполняется неравенство 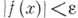 . Понятие Б. м. ф. может быть положено в основу общего определения предела функции. Именно, предел функции . Понятие Б. м. ф. может быть положено в основу общего определения предела функции. Именно, предел функции  при при  конечен и равен Атогда и только тогда, когда конечен и равен Атогда и только тогда, когда
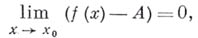
т. е. функция  - А есть Б. м. ф. См. также ст. Бесконечно малых исчисление. В. И. Битюцков. - А есть Б. м. ф. См. также ст. Бесконечно малых исчисление. В. И. Битюцков.
|

 , определенная в окрестности точки х 0, наз. бесконечно малой функцией при х, стремящемся к х 0 , если для любого числа
, определенная в окрестности точки х 0, наз. бесконечно малой функцией при х, стремящемся к х 0 , если для любого числа  найдется такое число
найдется такое число  , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется
, выполняется  . Этот факт записывается так:
. Этот факт записывается так:

 найдется такое
найдется такое  что Для всех
что Для всех  выполняется неравенство
выполняется неравенство 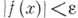 . Понятие Б. м. ф. может быть положено в основу общего определения предела функции. Именно, предел функции
. Понятие Б. м. ф. может быть положено в основу общего определения предела функции. Именно, предел функции  при
при  конечен и равен Атогда и только тогда, когда
конечен и равен Атогда и только тогда, когда 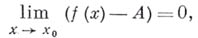
 - А есть Б. м. ф. См. также ст. Бесконечно малых исчисление. В. И. Битюцков.
- А есть Б. м. ф. См. также ст. Бесконечно малых исчисление. В. И. Битюцков.