|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОДЗначение ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД в математической энциклопедии: метод приближенного решения нелинейных функциональных уравнений. П. по п. м. состоит в том, что решаемое уравнение Р(х)=0 обобщается к виду F(x, t)=0 путем введения параметра t, принимающего заданные значения на конечном интервале Обобщенное уравнение F(x, t)=0 последовательно решается при отдельных значениях t: t0, t1, . . ., tk=t*. Уравнение при t=ti+1 решается каким-либо итерационным методом (методом Ньютона, простой итерации, итерационным методом вариации параметра [4] и др.), начиная с полученного решения х i уравнения F( х, t)=0 при t=ti. Применение на каждом шаге по i, напр, питераций метода Ньютона, приводит к следующей формуле: Если разность ti+1=ti достаточно мала, то значение xi может оказаться достаточно хорошим начальным приближением, обеспечивающим сходимость, для получения решения xi+1 при t=ti+1 (см. [1], [3], [5]). На практике часто исходная задача естественным образом зависит от нек-рого параметра, к-рый может быть выбран в качестве параметра t. П. по п. м. применяется как для решения систем нелинейных алгебраич. и трансцендентных уравнении (см. [1], [2]), так и для более общих нелинейных функциональных уравнений в банаховых пространствах (см. [5] - [7]). П. по п. м. иногда наз. также прямой метод вариации параметра (см. [2], [6]), а также комбинированный метод прямого и итерационного методов вариации параметра. В этих методах построение решений обобщенного уравнения сводится путем дифференцирования по параметру к решению дифференциальной задачи с начальными условиями (задачи Коши) методами численного интегрирования обыкновенных дифференциальных уравнений. Применяя простейший метод Эйлера в прямом методе вариации параметра к задаче Коши приближенные значения х(ti)= х i, i=l, 2, . . ., k, решения x(t).уравнения F(x, t)=0 можно определить следующими равенствами; Элемент х k будет искомым приближенным решением исходного уравнения Р(х)=0. Уточнение всех или нек-рых значений х i+1 можно проводить итерационным методом вариации параметра [4] (или методом Ньютона). Обобщенное уравнение при этом рассматривается обычно в виде на конечном промежутке Метод вариации параметра применен к широкому классу задач как для построения решений, так и для доказательства их существования (см., напр., [3], [4], 16], [7]). Лит.:[1] Lahaуе Е., "Acad. Roy. Belg. Bull., Cl. Soi. Ser. 5", 1948, t. 34, p. 809-27; [2] Давиденко Д. Ф., "Укр. матем. ж.", 1953, т. 5, №2, с. 196-206; [3] Ортега Дж., Рейнболдт В., Итерационные методы решения нелинейных систем уравнений со многими неизвестными, пер. с англ., М., 1975; [4] Давиденко Д. Ф., "Ж. вычисл. матем. и матем. физ.", 1975, т. 15, № 1, с. 30-47; [5] Дементьева А. М., "Докл. АН СССР", 1971, т. 201, М 4, с. 774 - 777; [6] Давиденко Д. Ф., "Укр. матем. ж.", 1955, т. 7, А" 1, с. 18-28; [7] Шидловская Н. А., "Уч. зап. ЛГУ", 1958, № 271, в. 33, с. 3 - 17. Д. Ф. Давиденко. |
|
|
|

 , так, что первоначальное уравнение получается при
, так, что первоначальное уравнение получается при  , а уравнение F( х, t0)=0 легко решается или известно его решение х 0 (см. [1] - [3]).
, а уравнение F( х, t0)=0 легко решается или известно его решение х 0 (см. [1] - [3]).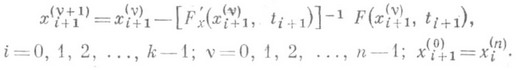



 или, заменяя здесь 1-l на е -t, на бесконечном промежутке
или, заменяя здесь 1-l на е -t, на бесконечном промежутке  .
.