|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОДЗначение ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД в математической энциклопедии: включение данной задачи в однопараметрическое (0 Пусть, напр., требуется доказать разрешимость в классе Гёльдера задачи Дирихле в ограниченной N-мерной области Вводится семейство эллиптич. операторов и рассматривается для него задача Дирихле Пусть П. по п. м. (в варианте аналитич. родолжения по параметру) был предложен и развит в ряде работ С. Н. Бернштейна (см. [1], [2]). В дальнейшем этот метод нашел широкое применение в различных вопросах теории линейных и нелинейных дифференциальных уравнений, причем идея аналитич. родолжения по параметру была дополнена более общими функциональными и топологич. принципами (см. [3]). Лит.:[1] Бернштейн С. Н., "Math. Ann.", 1904, Bd 59, S. 20-76; [2] его же, Собр. соч., т. 3, М., 1960; [3] Лерэ Ж., Шаудер Ю., "Успехи матеит. наук", 1946, в. 3/4, с. 71-95. И. А. Шишмарев. |
|
|
|

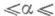 1) семейство задач, связывающее данную задачу (а=1) с известной разрешимой задачей (a=0), и изучение зависимости решений от параметра a. Метод широко используется в теории дифференциальных уравнений.
1) семейство задач, связывающее данную задачу (а=1) с известной разрешимой задачей (a=0), и изучение зависимости решений от параметра a. Метод широко используется в теории дифференциальных уравнений.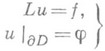 (1)
(1) для линейного эллиптич. оператора 2-го порядка
для линейного эллиптич. оператора 2-го порядка 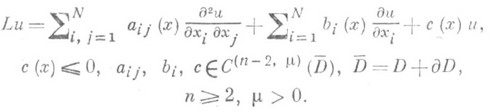
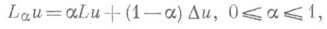
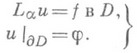 (2)
(2)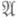 - множество тех
- множество тех 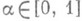 , для к-рых задача (2) однозначно разрешима в классе
, для к-рых задача (2) однозначно разрешима в классе 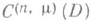 при любых f и
при любых f и 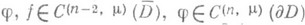 . Множество
. Множество 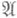 не пусто, поскольку при a=0 (т. е. для оператора Лапласа) задача (2) однозначно разрешима в классе
не пусто, поскольку при a=0 (т. е. для оператора Лапласа) задача (2) однозначно разрешима в классе 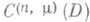 , как это следует из теории потенциала. Множество
, как это следует из теории потенциала. Множество 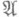 одновременно открыто и замкнуто на [0, 1] и; следовательно, совпадает с [0, 1]. Таким образом, a=1 принадлежит
одновременно открыто и замкнуто на [0, 1] и; следовательно, совпадает с [0, 1]. Таким образом, a=1 принадлежит  и задача (1) разрешима.
и задача (1) разрешима.