|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРОГРАММИРОВАНИЕ ТЕОРЕТИЧЕСКОЕЗначение ПРОГРАММИРОВАНИЕ ТЕОРЕТИЧЕСКОЕ в математической энциклопедии: математическая дисциплина, изучающая математич. абстракции программ, трактуемых как объекты, выраженные на формальном языке, обладающие определенной информационной и логич. структурой и подлежащие исполнению на автоматич. устройствах. П. т. сформировалось преимущественно на основе двух моделей вычислений: последовательных программ с памятью, или операторных программ, и рекурсивных программ. Обе модели строятся над нек-рой абстрактной алгебраич. системой <D, Ф, П>, образованной предметной областью D, конечным набором (сигнатурой) функциональных Ф={j1, . . ., j т} и предикатных П= {p1 ,. . ., pn} символов с заданным для каждого символа числом его аргументов (арностью). Определение класса программ слагается из трех частей: схемы программы (синтаксиса), интерпретации и семантики. Схема программы - это конструктивный объект, показывающий, как строится программа с использованием сигнатуры и других формальных символов. Интерпретация - это задание конкретной предметной области и сопоставление символам сигнатуры конкретных функций и предикатов (базовых операций), согласованных с предметной областью и арностью символов. Семантика - это способ сопоставления каждой программе результата ее выполнения. Как правило, с программами связывают вычисляемые ими функции. Интерпретация обычно входит в семантику как параметр, поэтому схема программы задает множество программ и вычисляемых ими функций, к-рое получается при варьировании интерпретаций над нек-рым запасом базовых операций. Схема программы с памятью, называемая также алголоподобной, или операторной, схемой, задается в виде конечного ориентированного графа переходов, имеющего обычно одну входную и одну выходную вершины, вершины с одной (преобразователи) и двумя (распознаватели) исходящими дугами. С помощью символов сигнатуры и счетного множества символов переменных и констант обычным образом строится множество функциональных и предикатных термов. Каждому распознавателю сопоставляется нек-рый предикатный терм, а преобразователю - оператор присваивания, имеющий вид y:=t, где у - символ переменной, а t - функциональный терм. Конечная совокупность всех переменных в схеме образует ее память. Интерпретация в дополнение к конкретизации базовых операций предписывает каждой переменной область ее изменения, а каждой константе - ее значение. Для программ с памятью наиболее обычна т. <н. операционная семантика, состоящая из алгоритма выполнения программы на заданном состоянии памяти. Программа выполняется при движении по графу переходов. При попадании на распознаватель вычисляется предикатный терм и происходит переход по дуге, соответствующей значению предиката. При попадании на преобразователь с оператором y:=t вычисляется значение t и присваивается переменной у. Результат выполнения программы - состояние памяти при попадании на выходную вершину. Схема рекурсивной программы, или рекурсивная схема, использует кроме функциональных т. н. условные термы, образующие вместе с первыми множество вычислительных термов. Условный терм задает вычисление методом разбора случаев и имеет вид (p|t1|t2), где p - предикатный, a t1 и t2 - вычислительные термы, и соответствует конструкции условного выражения в алголе: if p then t1 else t2. Термы строятся над счетным множеством входных и формальных переменных, констант и символов определяемых функций. Рекурсивная схема состоит из главного вычислительного терма с входными переменными и конечного набора рекурсивных уравнений вида f(xi, . . ., х п) -т, где f - символ определяемой функции, x1, . . ., х п - формальные переменные, а т - терм с переменными из множества {x1 ,. . ., х n} и с определяемыми функциями из набора уравнении. При естественных предположениях на интерпретацию базовых операций система уравнений относительно определяемых функций всегда имеет т. н. наименьшую неподвижную точку (н. н. т.) - совокупность функций, удовлетворяющих уравнениям, с графиками, принадлежащими графикам любых других решений уравнений. Подставляя в главный терм вместо символов определяемых функций соответствующие компоненты н. н. т., получают функциональный терм, задающий нек-рую функцию входных переменных, к-рая и объявляется функцией, вычисляемой рекурсивной программой. Поскольку такой способ сопоставления программе вычисляемой ею функции но дает конкретного алгоритма вычисления, определенная так семантика наз. денотационной. Указанные формализмы как бы отмечают диапазон уровней изобразительных средств языков программирования: если операторные схемы близки к структуре машинной программы, то рекурсивные схемы ближе кисходной формулировке задач, подлежащих программированию. Исследования по П. т. несут на себе отпечаток общематематич. средств, используемых при изучении моделей программ. Формально-комбинаторные методы формируют теорию схем программ, к-рая изучает свойства программ, инвариантные относительно выбора интерпретации базовых операций. Логич. методы изучают способы определения семантики программы, а также ищут закономерности в процессе построения программы. Алгебраич. методы, отвлекаясь от конкретной структуры программы, концентрируют свое внимание на изучении множеств, возникающих при рассмотрении программы или класса программ. Сложившиеся разделы П. т. охватывают в основном модели последовательных вычислений, выполняемых одним активным устройством. Изучение проблем, возникающих при необходимости организовать совместную работу ансамбля машин, объединяемых для решения одной задачи или взаимодействующих посредством передачи сигналов и информации, составляет предмет новой дисциплины - т. н. программирования параллельного. Теория схем программ. Отправным понятием теории схем программ является понятие функциональной эквивалентности. Две схемы функционально эквивалентны, если для любой интерпретации соответствующие программы вычисляют одинаковые функции. Каждому выполнению программы можно сопоставить его протокол - особого рода терм в сигнатуре базовых операций, отражающий порядок их выполнения. Если известны значения истинности предикатов, входящих в программу, то протокол по этим значениям строится однозначно, при этом для построения. не нужно знать интерпретации базовых операций. Если выбирать значения истинности предикатов произвольно, то в результате для схемы программы создается нек-рое множество формальных протоколов, называемое ее детерминантом. Две схемы формально эквивалентны, если их детерминанты совпадают. Формальная эквивалентность корректна, если из нее следует функциональная эквивалентность. Поскольку детерминант строится чисто комбинаторно на основе произвольного выбора из конечного множества, он образует формальный язык, воспринимаемый нек-рым автоматом. Представляют особый интерес такие определения протокола схем программ, к-рые приводят к разрешимым детерминантам. Для таких детерминантов можно ставить вопрос о поиске системы преобразований схем программ, полной в том смысле, что любые две формально эквивалентные схемы переводимы одна в другую этими преобразованиями. Структура теории схем программ сложилась на базе основополагающих работ А. А. Ляпунова и Ю. И. Янова (см. [5], [10]). Последний полностью изучил простейшую модель операторных схем с сигнатурой одноместных операций и допускающих в программе только одну неременную (схемы Янова). Протоколом схемы Янова является последовательность выполняемых операций, перемежаемых значениями предикатов. Автомат, воспринимающий детерминант, оказывается конечным автоматом, а формальная эквивалентность разрешима, при этом она совпадает с функциональной. Для схем Янова найдена полная система преобразований. Для общей модели операторных схем функциональная эквивалентность оказалась неразрешимой, однако удалось найти форму протокола - т. н. логико-термальную историю, к-рая приводит к разрешимому детерминанту. Этот протокол фиксирует последовательность выполнения и значения предикатов схемы, а для каждого аргумента предиката указывает функциональный терм, к-рый вычислял значение данного аргумента при выполнении программы. Автоматом, воспринимающим детерминант, оказывается двухленточный конечный автомат. Для логико-термальной формальной эквивалентности также найдена полная система преобразований. Существенное место в теории схем программ занимают вопросы перевода схем программ из одной вычислительной модели в другую. Операторные схемы эффективно переводятся в рекурсивные схемы в той же сигнатуре, однако обратная трансляция невозможна, т. к. выполнение рекурсивной программы требует, вообще говоря, сколь угодно большого числа ячеек памяти. Детерминант рекурсивной схемы может быть задан в виде контекстно-свободного языка (см. Грамматика бесконтекстная), однако вопрос о разрешимости соответствующей формальной эквивалентности остается пока (1983) открытым. Теория схем программ занимается также изучением отдельных классов схем программ с целью выделить случаи разрешимых эквивалентностей, она также обогащает базовую вычислительную модель дополнительными конструкциями языков программирования, изучая при этом выразительную силу обогащений и вопросы сводимости. Логическая теория программ. Говорят, что программа Ачастично правильна относительно входного условия Р и выходного условия Q(обозначение Р {А } Q), если в случае, когда Ристинно для входных значений переменных и Азавершает работу, Qистинно для выходных значений переменных. При этом Рназ. предусловием, a Q - постусловие м программы А. Программа А тотально правильна (обозначение Р<А>Q), если Ачастично правильна относительно Ри Q, а также Азавершает работу для входных значений переменных, удовлетворяющих условию Р. Для доказательства частичной правильности последовательных программ часто используется метод Флойда, к-рый состоит в следующем. На схеме программы выбираются контрольные точки так, чтобы любой циклич. путь проходил по крайней мере через одну точку. Контрольные точки также связываются с входом и выходом схемы. С каждой контрольной точкой ассоциируется специальное условие (т. <н. индуктивное утверждение, или инвариант цикла), к-рое истинно при каждом переходе через эту точку. С входной и выходной точками ассоциируются входное и выходное условия. Затем каждому пути программы между двумя соседними контрольными точками сопоставляется т. н. условие правильности. Выполнимость всех условий правильности гарантирует частичную правильность программы. Один из способов доказательства завершения работы программы состоит во введении в программу дополнительных счетчиков и установлении ограниченности этих счетчиков на выходе программы в процессе доказательства частичной правильности. Было предложено задавать аксиоматич. семантику языков программирования посредством конечной аксиоматич. системы (т. н. логики Xоара), состоящей из аксиом и правил вывода, в к-рой в качестве теорем выводимы утверждения о частичной правильности программ. Напр., для оператора присваивания схема аксиом имеет вид где (то есть Рявляется инвариантом цикла). Пусть рассматривается логика Хоара, у к-рой в качестве языка для записи условий взят язык арифметики 1-го порядка. Утверждение о частичной правильности программы наз. выводимым, если оно выводимо в расширении этой логики посредством добавления истинных формул арифметики, и наз. истинным, если оно истинно по отношению к операционной (или денотационной) семантике программы. Логика Хоара наз. состоятельной, если каждое выводимое в ней утверждение истинно, и наз. полной (относительно арифметики), если каждое истинное утверждение выводимо в ней. Состоятельная и полная логика Хоара построена, в частности, для языка программирования, содержащего простые переменные и операторы присваивания, составной, условный, цикла и процедуры (возможно, рекурсивные, но с рядом ограничений) . Важным обобщением логики Хоара является т. н. алгоритмическая (или динамическая) логика. Пусть P{A}Q представлено в виде Р Для доказательства утверждений о рекурсивных программах часто используется специальная индукция, связанная с определением н. н. т. Пусть для простоты рекурсивная программа задается одним уравнением f=t(f), а ее денотационная семантика - н. н. т. fH. При естественных предположениях об условии Рсправедлив следующий принцип индукцпи: если формула P(W). истинна и из Р(ti (W)) следует Р(ti+1 (W)), то выполняется Р(fH) (здесь W - нигде не определенная функция). Для описания денотационной семантики языков программирования высокого уровня используется задание области данных в виде т. н. полных решеток Скотта. Задачу синтеза программы можно формализовать как задачу построения доказательства теоремы Алгебраическая теория программ. Примером применения алгебраич. методов в П. т. может служить проблема эквивалентности дискретных преобразователей Глушкова, в к-рые естественно вкладываются операторные схемы программ. Пусть П. т. оказывает свое влияние на практику прежде всего как концептуальный багаж при изучении программирования и - более технич. путем - через теорию формальных языков программирования. Здесь свойства абстрактных моделей вычислений используются для уточнения семантики языков программирования и для обоснования различных манипуляций с программами (см. Трансляция программ, Программ оптимизирующие преобразования). Лит.:[1] Глушков В. М., Летичевский А. А., в кн.: Избранные вопросы алгебры и логики, Новосиб., 1973, о. 5-39; [2] Ершов А. П., Введение в теоретическое программирование, М., 1977; [3] Котов В. Е., Введение в теорию схем программ, Новосиб., 1978; [4] Лавров С. С., "Программирование", 1978, № 6, с. 3-10; [5] Ляпунов А. А., "Проблемы кибернетики", 1958, в. 1, с. 46-74; [6] Непейвода Н. Н., "Программирование", 1979, М 1, с. 15-25; [7] Плюшкявичюс Р. А.; [и др.], "Кибернетика", 1979, № 2, с. 12-19; [8] Семантика языков программирования. Сб. статей, пер. с англ., М., 1980; [9] Скотт Д., "Кибернетический сборник", 1977, в. 14, с. 107-21; [10] Янов Ю. И., "Проблемы кибернетики", 1958, в. 1, с. 75-127; [11] Manna Z., Mathematical theory of computation, N.Y., - [а. <о.], 1974. А. П. Ершов, В. А. Непомнящий. |
|
|
|

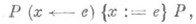
 означает результат подстановки в Рвыражения евместо всех вхождений переменной х, а для оператора цикла типа while правило вывода имеет вид
означает результат подстановки в Рвыражения евместо всех вхождений переменной х, а для оператора цикла типа while правило вывода имеет вид 
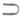 [A]Q, где [A]Qесть самое слабое предусловие, для к-рого справедливо утверждение о частичной правильности программы Ас постусловием Q. Аналогично для случая тотальной правильности пусть P<A>Q представлено в виде Р
[A]Q, где [A]Qесть самое слабое предусловие, для к-рого справедливо утверждение о частичной правильности программы Ас постусловием Q. Аналогично для случая тотальной правильности пусть P<A>Q представлено в виде Р  <А>Q. Формулы алгоритмич. логики строятся из формул базового логич. языка (для записи условий) и программ с помощью булевых операций, кванторов, а также операций вида [A]<Q, <А>Q. В алгоритмич. логике выразимы различные утверждения о программах, напр, их эквивалентность. Аналогично логике Хоара для алгоритмич. логики построена состоятельная и полная конечная аксиоматич. система в случае языка программирования, допускающего и недетерминированные программы.
<А>Q. Формулы алгоритмич. логики строятся из формул базового логич. языка (для записи условий) и программ с помощью булевых операций, кванторов, а также операций вида [A]<Q, <А>Q. В алгоритмич. логике выразимы различные утверждения о программах, напр, их эквивалентность. Аналогично логике Хоара для алгоритмич. логики построена состоятельная и полная конечная аксиоматич. система в случае языка программирования, допускающего и недетерминированные программы. и последующего извлечения программы из этого доказательства. Построен алгоритм, к-рый по доказательству в интуиционистской логике дает программу на языке алгол-68. Если доказательство использует правило индукции, то ему соответствует в программе цикл вида for to ... do ... od. Извлекаемая программа будет приемлемой сложности, если использовать предположение, что она строится из стандартных (т. е. заданных) функций и предикатов, свойства к-рых описаны аксиомами специального вида.
и последующего извлечения программы из этого доказательства. Построен алгоритм, к-рый по доказательству в интуиционистской логике дает программу на языке алгол-68. Если доказательство использует правило индукции, то ему соответствует в программе цикл вида for to ... do ... od. Извлекаемая программа будет приемлемой сложности, если использовать предположение, что она строится из стандартных (т. е. заданных) функций и предикатов, свойства к-рых описаны аксиомами специального вида. - конечный автомат Мили с входным алфавитом Xи выходным алфавитом Y и с заданными начальным и заключительным состояниями. Пусть G - полугруппа с множеством образующих Yи единицей е. Пусть рассматривается автомат Мура Gm, (возможно, бесконечный) с множествами состояний G, входов Y, выходов X, начальным состоянием е, функцией выходов m(g). и функцией переходов q(g, y)=gy. Автомат
- конечный автомат Мили с входным алфавитом Xи выходным алфавитом Y и с заданными начальным и заключительным состояниями. Пусть G - полугруппа с множеством образующих Yи единицей е. Пусть рассматривается автомат Мура Gm, (возможно, бесконечный) с множествами состояний G, входов Y, выходов X, начальным состоянием е, функцией выходов m(g). и функцией переходов q(g, y)=gy. Автомат  , работающий совместно с Gm, наз. дискретным преобразователем, если
, работающий совместно с Gm, наз. дискретным преобразователем, если 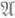 воспринимает в качестве входа выход Gm, а воспринимает в качестве входа выход
воспринимает в качестве входа выход Gm, а воспринимает в качестве входа выход  . Выходом
. Выходом  считается при этом состояние Gm в момент остановки
считается при этом состояние Gm в момент остановки  . Дискретные преобразователи эквивалентны относительно полугруппы G, если для каждого отображения m из G в Xони оба не останавливаются при работе с Gm либо оба останавливаются с одинаковым выходом. Установлена разрешимость проблемы эквивалентности дискретных преобразователей относительно полугруппы с левым сокращением, неразложимой единицей, в к-рой разрешима проблема тождества слов. Описаны также все разрешимые и неразрешимые случаи эквивалентности дискретных преобразователей относительно коммутативной полугруппы.
. Дискретные преобразователи эквивалентны относительно полугруппы G, если для каждого отображения m из G в Xони оба не останавливаются при работе с Gm либо оба останавливаются с одинаковым выходом. Установлена разрешимость проблемы эквивалентности дискретных преобразователей относительно полугруппы с левым сокращением, неразложимой единицей, в к-рой разрешима проблема тождества слов. Описаны также все разрешимые и неразрешимые случаи эквивалентности дискретных преобразователей относительно коммутативной полугруппы.