|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРИСТРЕЛКИ МЕТОДЗначение ПРИСТРЕЛКИ МЕТОД в математической энциклопедии: стрельбы метод,- метод решения краевой задачи для обыкновенного дифференциального уравнения, к-рый заключается во введении управляющих переменных (параметров) и последующем нахождении их из системы уравнений, при этом выбор параметров имеет решающее значение для успешного решения задачи. Пусть имеется при где вектор-функция где относительно параметра r. Алгоритм П. м. состоит в следующем: сначала находят решение r=r * уравнения (5), а затем - искомое решение граничной задачи (1) - (2) как решение задачи Коши Для решения упоминавшихся здесь задач Коши могут быть использованы численные методы. Для решения уравнения (5) целесообразно избрать какой-либо итерационный метод. В случае, когда нек-рые из компонент вектора gзависят только от у(а), а остальные компоненты - только от у(b), выгоден другой выбор параметров (см. [1], а также Нелинейная краевая задача;численные методы решения). Имеются другие варианты П. м. (см. [4]). П. м. применяют и при решении сеточной краевой задачи. Лит.:[1] Бахвалов Н. С., Численные методы, 2 изд., М., 1975; [2] Годунов С. К., Рябенький В. С., Разностные схемы, 2 изд., М., 1977; [3] Крылов В. И., Бобков В. В., Монастырный П. И., Вычислительные методы, т. 2, М., 1977; [4] Современные численные методы решения обыкновенных дифференциальных уравнений, пер. с англ., М., 1979. А. Ф. Шапкин. |
|
|
|

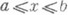 дифференциальное уравнение
дифференциальное уравнение  (1) с граничным условием
(1) с граничным условием  (2)
(2) от хподлежит определению, вектор-функции
от хподлежит определению, вектор-функции  и g
и g известны, числовой вектор
известны, числовой вектор 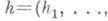
 задан. Пусть задача Коши
задан. Пусть задача Коши 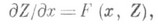 (3)
(3)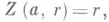 (4)
(4)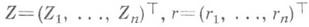 , имеет единственное решение Z( х, r), определенное при
, имеет единственное решение Z( х, r), определенное при 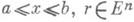 При подстановке в (2) вместо у(а).заданного значения Z(a, r)=r, а вместо у(b).найденного значения Z(b, r).получают уравнение
При подстановке в (2) вместо у(а).заданного значения Z(a, r)=r, а вместо у(b).найденного значения Z(b, r).получают уравнение  (5)
(5)