|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРИБЛИЖЕНИЕ ФУНКЦИЙЗначение ПРИБЛИЖЕНИЕ ФУНКЦИЙ в математической энциклопедии: экстремальные задачи на классах функций - задачи, связанные с отысканием верхней грани погрешности приближения на фиксированном классе функций и с выбором для него наилучшего в том или ином смысле аппарата приближения. Начало исследованиям по экстремальным задачам П. ф. положили работы А. Н. Колмогорова (см. [1] - [2]), Ж. Фавара (см. [3] - [4]) и С. М. Никольского (см. [5]-[6]). Широкое развитие эти исследования получили начиная с 50-х гг. 20 в.; они стимулировались потребностями вычислительной математики, все больше сталкивавшейся с задачами оптимизационного содержания. Если в нормированном функциональном пространстве Xрассматривается П. ф. из класса где - наилучшее приближение функции f(t)множеством где U - нек-рый конкретный метод приближения, задаваемый тем или иным оператором, действующим из X в распространенную на все линейные ограниченные операторы Uиз Xв и, естественно, возникает вопрос о возможности здесь знака равенства. Помимо тривиального случая, когда X - гильбертово пространство функций и наилучшее приближение каждой функции доставляют суммы Фурье по ортонормированному базису Так, если X - пространство 2p-периодических функций где К r- константы Фавара, причем наилучшее приближение на классах Для приближения подпространством наилучшим линейным методом здесь являются сплайны sr-1(f, t).из Перечисленные случаи, когда величины (1) и (3) совпадают и удается построить конкретный линейный метод, решающий сразу обе задачи, являются, в известном смысле, идеальными. В других ситуациях эффективным при решении задачи (1) оказывается подход, основанный на использовании общих теорем двойственности, отражающих фундаментальные соотношения геометрии выпуклого анализа (см. [7], [8]). Если, напр., X - произвольное линейное нормированное пространство, X*- ему сопряженное, Соотношения (4) или (5) позволяют в ряде случаев свести вычисление или оценку верхней грани (1) к более обозримой задаче на экстремум явно задаваемого функционала на нек-ром множестве функций, связанных, если
неравенств к вычислению верхней грани норм ||g||q'(q' =q/(q-1)) на множестве функций Более тонкая ситуация возникает, если задача (1) решается на классах, задаваемых ограничениями не на норму r-й производной f(r)(t) а на ее модуль непрерывности где w(d) - заданный модуль непрерывности, напр. где у к-рой где функции Ф k(t)задаются на [0, p] рекуррентно: Решение задач о наилучшем для класса Интерполяционные сплайны sr(f, t).из При решении экстремальных задач на классах функций, заданных на конечном отрезке и не связанных жесткими краевыми условиями, нельзя ждать результатов в столь совершенном, как в периодич. случае, виде: на экстремальных функциях сказывается возмущающее действие концов промежутка, к-рое усугубляется с увеличением порядка дифференцируемости. Здесь известны нек-рые результаты с точной асимптотикой. Если MWrHa(r=0,l,. . .; то для наилучшего равномерного на [-1, 1] приближения подпространством к-рые полезно сравнить с соответствующими результатами в периодич. случае; при a=1 правые части (6) и (7) равны соответственно МК 1 и MKr+1. Отказавшись от многочленов наилучшего приближения, можно усилить эти результаты, существенно улучшив приближение у концов отрезка [- 1, 1] без потери наилучшей асимптотики на всем промежутке. Напр., для любой Аналогичный факт имеет место для функций классов MWrH1(r=1, 2, . . .) (см. [11]). В задачах приближения сплайнами (наилучшими и интерполяционными) классов функций, заданных на отрезке, известны нек-рые точные (гл. обр., для сплайнов малого порядка) и асимптотически точные результаты (см. [15]). В случае одностороннего приближения (в интегральной метрике) известен ряд точных результатов по оценке погрешности наилучшего приближения полиномами и сплайнами на введенных выше классах функций (см. [19]). При их получении существенно использовались соотношения двойственности для наилучшего приближения при наличии ограничений, задаваемых с помощью конуса. Отыскание наилучшего аппарата приближения (фиксированной размерности) для данного класса функций
где нижние грани берутся по всем подпространствам а при выпуклом вверх w(d) и Следует отметить, что подпространство Задачу оценки погрешности приближения на множестве Х r r -х интегралов от функций из X(не являющемся локально компактным) можно сделать корректной, если оценивать для (w(g, d)X - модуль непрерывности функции gв пространстве X).или (в случае приближения конкретным методом) величину Отыскание точных верхних граней этих величин на множестве Х r равносильно нахождению наименьшей константы в соответствующем Джексона неравенстве;можно затем говорить о минимизации по всем подпространствам размерности N. В ряде случаев эти задачи решены. Напр., в неравенстве наименьшая константа М r= К r/2, причем она не может быть уменьшена, если Среди экстремальных задач, в к-рых приближающее множество, не будучи линейным многообразием, является выпуклым множеством, интерес представляют задачи наилучшего приближения одного класса функций (см. [7]); в дальнейшем ее стали рассматривать как самостоятельную, причем в ряде случаев использование соотношения (4) позволило получить точный результат. При здесь обнаруживается связь с задачами о неравенствах между нормами производных и о наилучшем приближении оператора дифференцирования линейными ограниченными операторами (см. [16]). Многие экстремальные задачи приближения функций можно интерпретировать как задачи оптимального восстановления (см. [15], [17], [18]). Пусть информация о функции Лит.:[1] Колмогоров А. Н., "Ann. Math.", 1935, v. 36, № 2, с. 521-26; [2] его же, там же, 1936, у. 37, № 1, р. 107-10; [3] Favard J., "С. г. Acad. sci.", 1936, t. 203, p. 1122-24; [4] его же, "Bull. sci. math.", 1937, t. 61, p. 209-24, 243-56; [5] Никольский С. М., "Тр. МИАН СССР", 1945, т. 15, с. 1-76; [6] его же, "Изв. АН СССР. Сер. матем.", 1946, т. 10, с. 207-56; [7] Корнейчук Н. П., Экстремальные задачи теории приближения, М., 1976; [8] Тихомиров В. М., Некоторые вопросы теории приближений, М. г 1976; [9] Дзядык В. К., Введение в теорию равномерного приближения функций полиномами, М., 1977; [10] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [11] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960; [12] Степанец А. И., Равномерные приближения тригонометрическими полиномами. Линейные методы, К., 1981; [13] Корнейчук Н. П., "Матем. заметки", 1976, т. 20, №5, с. 655-64; [14] его же, "Укр. матем. журн.", 1979, т. 31, № 4, с. 380-88; [15] его же, "Изв. АН СССР. Сер. матем.", 1981, т. 45, №2, с. 266-90; [16] Арестов В. В., "Тр. Матем. ин-та АН СССР", 1975, т. 138, с. 3-28; [17] Великий В. Л., "Матем. заметки", 1977, т. 22, № 5, с. 663-70; [18] Лигун A. A., "Anal. Math.", 1979, у. 5, М 4, р. 269-86; [19] Корнейчук Н. П., Лигун А. А., Доронин В. Г., Аппроксимация с ограничениями, К., 1982. Н. П. Корнейчук. |
|
|
|

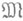 функциями фиксированного множества
функциями фиксированного множества  , то интерес представляют задачи отыскания величин
, то интерес представляют задачи отыскания величин 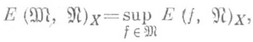 (1)
(1)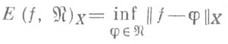
 , а также
, а также  (2)
(2)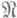 . Сгеометрич. точки зрения верхняя грань (1) характеризует величину уклонения множества
. Сгеометрич. точки зрения верхняя грань (1) характеризует величину уклонения множества 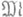 от
от  в метрике X. Практич. смысл величины
в метрике X. Практич. смысл величины 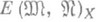 можно видеть в том, что она, во-первых, дает минимально возможную оценку сверху для наилучшего приближения множеством
можно видеть в том, что она, во-первых, дает минимально возможную оценку сверху для наилучшего приближения множеством  функции, о к-рой известно только, что она принадлежит классу
функции, о к-рой известно только, что она принадлежит классу 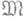 , а во-вторых, является определенным ориентиром при оценке и сравнении аппроксимативных возможностей конкретных методов приближения на классе
, а во-вторых, является определенным ориентиром при оценке и сравнении аппроксимативных возможностей конкретных методов приближения на классе  . Что касается величины (2), то наиболее важным является случай, когда
. Что касается величины (2), то наиболее важным является случай, когда  есть N-мерное подпространство, U - линейный метод приближения. Известен целый ряд точных и асимптотически точных результатов по приближению классов функций конкретными линейными .методами (в частности, полиномами и сплайнами) (см. [1]-[12], [19]), но особый интерес вызывают методы, реализующие точную нижнюю грань
есть N-мерное подпространство, U - линейный метод приближения. Известен целый ряд точных и асимптотически точных результатов по приближению классов функций конкретными линейными .методами (в частности, полиномами и сплайнами) (см. [1]-[12], [19]), но особый интерес вызывают методы, реализующие точную нижнюю грань 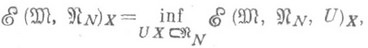 (3)
(3)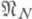 , т. е. линейные методы, наилучшие для класса
, т. е. линейные методы, наилучшие для класса 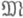 . Ясно, что всегда
. Ясно, что всегда 
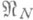 , известны ситуации в негильбертовом пространстве, когда линейный метод реализует наилучшее приближение на всем классе
, известны ситуации в негильбертовом пространстве, когда линейный метод реализует наилучшее приближение на всем классе 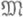
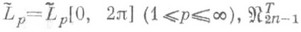 - подпространство тригонометрич. полиномов порядка n-1(dim
- подпространство тригонометрич. полиномов порядка n-1(dim =2n-1),
=2n-1), 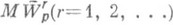 - класс функций
- класс функций 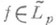 , у к-рых f(r-1)(t).абсолютно непрерывна на [0,2p] и
, у к-рых f(r-1)(t).абсолютно непрерывна на [0,2p] и 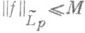 , то
, то 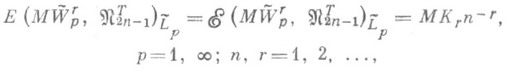
 и
и 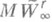 реализует линейный метод
реализует линейный метод 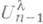 , построенный на базе сумм Фурье (см. Приближение функций;линейные методы приближения, формула (3)) при определенном выборе множителей
, построенный на базе сумм Фурье (см. Приближение функций;линейные методы приближения, формула (3)) при определенном выборе множителей 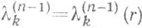 . Построены линейные операторы со значениями в
. Построены линейные операторы со значениями в 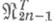 , реализующие верхнюю грань наилучших приближений на классах сверток, включающих, в частности, классы
, реализующие верхнюю грань наилучших приближений на классах сверток, включающих, в частности, классы  и
и 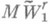 с дробными r>0, а также классы сопряженных функций (см. [10], [11]).
с дробными r>0, а также классы сопряженных функций (см. [10], [11]).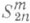 2p-периодических сплайнов порядка тдефекта 1 с узлами склей ки kp/n(dim
2p-периодических сплайнов порядка тдефекта 1 с узлами склей ки kp/n(dim 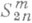 =2n).справедливы равенства
=2n).справедливы равенства 
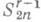 , интерполирующие функцию f(t).в точках kp/n, если r четно, и в точках kp/n+p/2n, если rнечетно. Относительно класса
, интерполирующие функцию f(t).в точках kp/n, если r четно, и в точках kp/n+p/2n, если rнечетно. Относительно класса 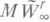 эти сплайны обладают исключительными аппроксимативными свойствами, т. к. наилучшим образом приближают функции
эти сплайны обладают исключительными аппроксимативными свойствами, т. к. наилучшим образом приближают функции 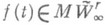 в любой метрике
в любой метрике 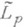 (см. [7]).
(см. [7]).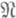 - выпуклое множество в X, то для любого элемента
- выпуклое множество в X, то для любого элемента 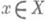
 (4) в частности, если
(4) в частности, если  - подпространство, то
- подпространство, то 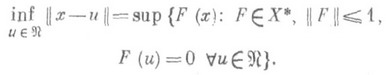 (5)
(5)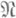 - подпространство, условиями ортогональности. Например, используя (5), оценку можно свести с помощью известных
- подпространство, условиями ортогональности. Например, используя (5), оценку можно свести с помощью известных 
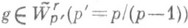 таких, что
таких, что 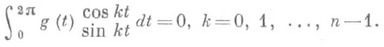
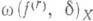 , в частности когда
, в частности когда  (r=0,1,...;
(r=0,1,...; 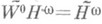 ) - класс 2p-периодических функций
) - класс 2p-периодических функций  , у к-рых
, у к-рых 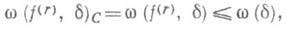
 . Здесь применение (5) требует использования тонких свойств дифференцируемых периодич. функций тина теорем сравнения и Колмогорова неравенств (для норм производных), но описываемых с помощью аппарата перестановок (равноизмеримых функций). При условии выпуклости вверх w(d) справедливы равенства (см. [7], [13])
. Здесь применение (5) требует использования тонких свойств дифференцируемых периодич. функций тина теорем сравнения и Колмогорова неравенств (для норм производных), но описываемых с помощью аппарата перестановок (равноизмеримых функций). При условии выпуклости вверх w(d) справедливы равенства (см. [7], [13])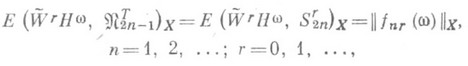
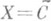 или
или 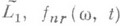 - функция из
- функция из 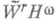 периода 2p/п с нулевым средним значением на периоде,
периода 2p/п с нулевым средним значением на периоде,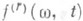 четна, равна
четна, равна 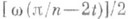 на [0, p/2n] и равна
на [0, p/2n] и равна 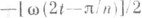 на
на  . Нормы
. Нормы 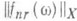 допускают явное выражение, напр.:
допускают явное выражение, напр.: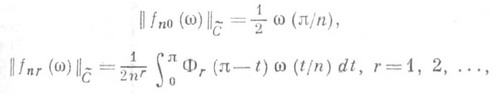
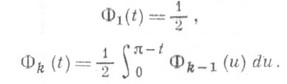
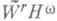 линейном методе из
линейном методе из 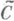 в
в 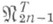 или в
или в 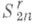 известно в случае
известно в случае 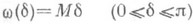 , т. е. когда
, т. е. когда 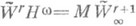
 реализуют верхнюю грань
реализуют верхнюю грань 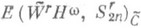 (при любом выпуклом w(d)) лишь в случае r=1.
(при любом выпуклом w(d)) лишь в случае r=1.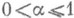 , MW0Ha=МНa).- класс функций
, MW0Ha=МНa).- класс функций 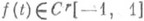 , у к-рых
, у к-рых 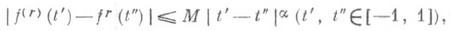
 алгебраич. многочленов степени п-1 имеют место соотношения
алгебраич. многочленов степени п-1 имеют место соотношения 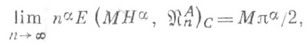 (6)
(6) (7)
(7)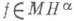 существует последовательность алгебраич. многочленов
существует последовательность алгебраич. многочленов  таких, что равномерно по
таких, что равномерно по  при
при 
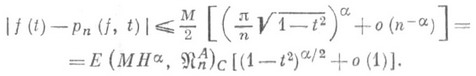
 приводит к задачам о поперечниках: найти величины (см. (1) и (3))
приводит к задачам о поперечниках: найти величины (см. (1) и (3))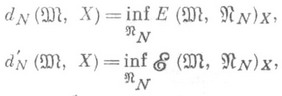
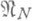 из X (и их сдвигам) размерности N, а также указать экстремальные (наилучшие) подпространства, реализующие эти нижние грани. Оценки сверху для dN и
из X (и их сдвигам) размерности N, а также указать экстремальные (наилучшие) подпространства, реализующие эти нижние грани. Оценки сверху для dN и 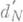 дают найденные для конкретных подпространств
дают найденные для конкретных подпространств 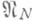 величины
величины  и
и  , основная трудность в задаче о поперечнике обычно состоит в получении точных оценок снизу. В ряде ситуаций получить такие оценки удается, привлекая топологич. соображения, в частности теорему Борсука об антиподах (см. [8]). Практически во всех случаях точного решения задачи о наилучшем приближении классов
, основная трудность в задаче о поперечнике обычно состоит в получении точных оценок снизу. В ряде ситуаций получить такие оценки удается, привлекая топологич. соображения, в частности теорему Борсука об антиподах (см. [8]). Практически во всех случаях точного решения задачи о наилучшем приближении классов 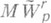 и
и  периодич. функций подпространствами
периодич. функций подпространствами 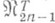 (тригонометрич. полиномов порядка п-1) и
(тригонометрич. полиномов порядка п-1) и 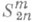 (сплайнов нек-рого порядка тдефекта 1 по разбиению kp/n). найденные точные верхние грани Е(
(сплайнов нек-рого порядка тдефекта 1 по разбиению kp/n). найденные точные верхние грани Е( ,
,  )X дают и значения поперечников dN этих классов, причем оказалось, что для периодич. классов d2n-1=d2n. В частности (см. [7], [8]) ,
)X дают и значения поперечников dN этих классов, причем оказалось, что для периодич. классов d2n-1=d2n. В частности (см. [7], [8]) ,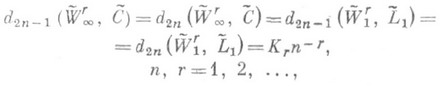
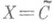 или
или 
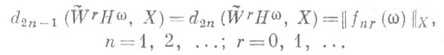
 является наилучшим для рассматриваемых классов при всех r и никакое подпространство размерности 2п не дает на этих классах лучшее приближение, чем
является наилучшим для рассматриваемых классов при всех r и никакое подпространство размерности 2п не дает на этих классах лучшее приближение, чем 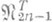 (имеющее размерность 2п-1). Подпространство сплайнов
(имеющее размерность 2п-1). Подпространство сплайнов 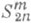 является наилучшим для классов
является наилучшим для классов  и
и 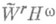 в
в 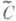 при т=r и для класса
при т=r и для класса 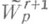 в
в 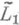 при
при  . Линейные поперечники
. Линейные поперечники 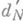 классов
классов 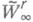 в
в 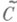 и
и 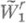 в
в 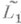 совпадают с dN, они реализуются на подпространствах
совпадают с dN, они реализуются на подпространствах 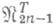 и
и 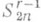 наилучшими линейными методами, о к-рых упоминалось выше. Поперечники dN и
наилучшими линейными методами, о к-рых упоминалось выше. Поперечники dN и 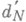 класса
класса 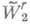 в
в 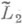 при N=2n-1 и N=2n равны и реализуются суммами Фурье по тригонометрич. системе. Для поперечников классов функций, заданных на отрезке, в ряде случаев известна точная асимптотика; поперечники dN и
при N=2n-1 и N=2n равны и реализуются суммами Фурье по тригонометрич. системе. Для поперечников классов функций, заданных на отрезке, в ряде случаев известна точная асимптотика; поперечники dN и 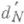 классов
классов 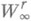 в С[-1, 1] совпадают и реализуются интерполяционными сплайнами порядка r -1 по неравномерному разбиению (см. [8]).
в С[-1, 1] совпадают и реализуются интерполяционными сплайнами порядка r -1 по неравномерному разбиению (см. [8]).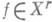 при фиксированном g>0 величину
при фиксированном g>0 величину 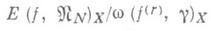
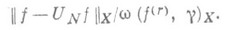

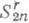 заменить любым другим подпространством той же размерности (см. [14]). Известны точные константы в неравенстве Джексона для приближения тригонометрич. полиномами в равномерной и интегральной метрике (см. [7]). В непериодич. случае есть результаты с точной асимптотикой.
заменить любым другим подпространством той же размерности (см. [14]). Известны точные константы в неравенстве Джексона для приближения тригонометрич. полиномами в равномерной и интегральной метрике (см. [7]). В непериодич. случае есть результаты с точной асимптотикой.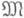 другим классом
другим классом 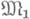 с лучшими, в том или ином смысле, гладкостными свойствами. Сначала такая задача возникла как промежуточная при получении точной оценки для
с лучшими, в том или ином смысле, гладкостными свойствами. Сначала такая задача возникла как промежуточная при получении точной оценки для 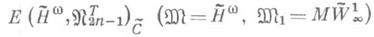
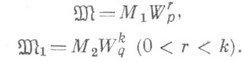
 задается вектором T(f,L)=(l1(f), ... ,ln(f)}, где lk - заданные на Xфункционалы (напр., значения функции f(t).или (и) нек-рых ее производных в фиксированных точках). Зная, что f принадлежит классу
задается вектором T(f,L)=(l1(f), ... ,ln(f)}, где lk - заданные на Xфункционалы (напр., значения функции f(t).или (и) нек-рых ее производных в фиксированных точках). Зная, что f принадлежит классу  , требуется по информации T(f,L) восстановить с наименьшей погрешностью функцию f или значение L(f) на ней нек-рого линейного функционала (напр.,
, требуется по информации T(f,L) восстановить с наименьшей погрешностью функцию f или значение L(f) на ней нек-рого линейного функционала (напр.,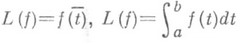 и т. п.). Минимизация может предполагаться не только по методам S, сопоставляющим вектору T(f,L) функцию j(t)
и т. п.). Минимизация может предполагаться не только по методам S, сопоставляющим вектору T(f,L) функцию j(t)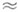 f(t). (или функционал l(f)
f(t). (или функционал l(f) L(f)), но также и по наборам функционалов
L(f)), но также и по наборам функционалов  . В зависимости от выбора меры погрешности и класса методов Sзадача оптимального восстановления функции может быть иногда сведена к отысканию поперечников dN или
. В зависимости от выбора меры погрешности и класса методов Sзадача оптимального восстановления функции может быть иногда сведена к отысканию поперечников dN или  , чебышевского центра или других характеристик класса
, чебышевского центра или других характеристик класса  . Оптимальное восстановление интеграла
. Оптимальное восстановление интеграла 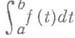 по информации вида {f(tk)} или {f(v)(tk)} приводит к задаче о наилучшей квадратурной формуле для класса
по информации вида {f(tk)} или {f(v)(tk)} приводит к задаче о наилучшей квадратурной формуле для класса  . Наилучший аппарат восстановления в ряде случаев доставляют сплайны; так, напр., сплайны sr-1(f, t).из
. Наилучший аппарат восстановления в ряде случаев доставляют сплайны; так, напр., сплайны sr-1(f, t).из  , интерполирующие в равностоящих точках tk, восстанавливают функции f из
, интерполирующие в равностоящих точках tk, восстанавливают функции f из 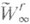 по информации lk(f)=f(tk) в каждой точке
по информации lk(f)=f(tk) в каждой точке  с минимально возможной на всем классе
с минимально возможной на всем классе 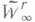 погрешностью. В пространствах функций двух и большего числа переменных, если не считать тривиального случая приближения в гильбертовом пространстве, точных решений экстремальных задач почти нет (1983). В немногих случаях известны асимптотически точные соотношения для погрешности равномерного приближения классов функций суммами Фурье и нек-рыми их средними (см. [12]).
погрешностью. В пространствах функций двух и большего числа переменных, если не считать тривиального случая приближения в гильбертовом пространстве, точных решений экстремальных задач почти нет (1983). В немногих случаях известны асимптотически точные соотношения для погрешности равномерного приближения классов функций суммами Фурье и нек-рыми их средними (см. [12]).