|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРИБЛИЖЕНИЕ ФУНКЦИЙЗначение ПРИБЛИЖЕНИЕ ФУНКЦИЙ в математической энциклопедии: замена по определенному правилу функции f(t).близкой к ней в том или ином смысле функцией j(t). из заранее фиксированного множества Практич. необходимость в П. ф. возникает в самых различных ситуациях, когда нужно функцию f(t).заменить более гладкой или более простой и удобной для вычислений, восстановить функциональную зависимость по экспериментальным данным и т. п. В общей задаче П. ф. обычно можно выделить следующие более частные задачи: выбор приближающего множества При выборе приближающего множества Классич. аппаратами приближения являются алгебраические (если Q- ограниченное замкнутое множество) и тригонометрические (в периодич. случае) полиномы одного и многих переменных. Широкое применение их в качестве приближающего множества обусловлено, в частности, принципиальной возможностью приблизить непрерывную функцию алгебраическими или тригонометрич. полиномами с любой наперед заданной погрешностью. Точность приближения может быть повышена за счет увеличения степени полинома, что, однако, усложняет приближающий аппарат и увеличивает вычислительные трудности при его использовании. На практике в качестве приближающего множества берут подпространства алгебраических или тригонометрич. полиномов фиксированного порядка и стремятся получить нужную точность с помощью полиномов возможно меньшей степени. Более общий и в то же время более гибкий аппарат приближения получают, рассматривая обобщенные полиномы где {j1, . . .,jN} - нек-рая система линейно независимых функций, к-рую можно выбирать в зависимости от условий конкретной задачи и априорных требований на j(t). Во многих задачах более естественным и удобным с вычислительной точки зрения, чем классич. полиномы, аппаратом приближения оказались сплайны. Если фиксированное разбиение отрезка [а, b], то (полиномиальным) сплайном порядка гдефекта k(k=l, 2, ..., r).по разбиению DN наз. функцию s(t),"склеенную" в точках t1, t2, ..., tN-1 из алгебраич. многочленов степени rтак, что на всем отрезке [а, b]она непрерывна вместе со своими производными до (r-k )-го порядка включительно. Таким образом, s(t) Если f(t).имеет особенности или приближение осуществляется в неограниченной области, то удобным аппаратом приближения являются рациональные дроби p(t)/q(t), где p(t).и q(t) - алгебраич. многочлены. Заданные на всей действительной оси непериодич. функции приближают также целыми функциями экспоненциального типа. Мера погрешности m(f, j) выбирается обычно с учетом условий конкретной задачи и имеющейся информации о приближаемой функции f(t). Чаще всего дело сводится к выбору содержащего f функционального пространства, в метрике к-рого целесообразно оценивать погрешность приближения. Если то речь идет оравно мерном, или чебышевском, приближении, если же то говорят о среднестепенном приближении, к-рое при р=1 наз. приближением в среднем. Особое значение имеет случай р=2 - средне к вадратическое приближение, когда погрешность наилучшего приближения функции f конечномерным подпространством может быть точно выражена через нек-рые определители. В нек-рых задачах требования близости функций f и j в различных точках различны; для учета этой неоднородности вводят весовую функциюr(t) или Весовая функция позволяет также обеспечить конечность погрешности, если, напр., f(t).ноограничена. Если погрешность должна учитывать близость f и j только в отдельных точках tk(k=1, . . ., N).из Q, то в качестве m (f, j) можно выбрать одну из величин или в к-рые также могут вводиться весовые коэффициенты. При решении вопроса о том, по какому правилу выбирать из множества Здесь сразу же возникают вопросы о существовании и единственности такой функции (функции наилучшего приближения), а также о ее характеристич. свойствах (см. [5]). Существование гарантируется, если Если принадлежит Интерполирование сплайнами имеет свои особенности, связанные с выбором точек интерполяции и краевых условий, обеспечивающих существование и единственность интерполяционного сплайна. Напр., сплайн s(t).порядка В П. ф. важную роль играют также линейные методы, построенные на базе разложения приближаемой функции в ряд Фурье по нек-рой ортогональной системе. В частности, в периодич. случае широко распространенным аппаратом приближения являются суммы Фурье по тригонометрич. системе и их различные усреднения (см. Приближение функций;линейные методы приближения). Исследование и оценка погрешности приближения - важный с практич. точки зрения и в то Же время наиболее содержательный в идейном отношении этап П. ф. Именно разработка методов оценки погрешности, Изучение зависимости ее от гладкостиых характеристик приближаемой функции, исследование и сравнение аппроксимативных свойств различных аппаратов приближения привели к формированию теории приближения функций - одного из наиболее интенсивно развивающихся разделов математич. анализа. Фундамент теорий П. ф. был заложен работами П. Л. Чебыгаева в 1854-59 (см. [1]) о наилучшем равномерном приближении непрерывных функций многочленами и рациональными дробями, а также работами К. Вейерштрасса [2], доказавшего в 1885, что для любой непрерывной на отрезке [ а, b] или непрерывной на всей оси с периодом 2p функции f(t).существует последовательность алгебраических (соответственно тригонометрических) полиномов Pn(f, t).порядка n=1, 2, ... такая, что при где Qесть [ а, b]или, соответственно, вся числовая ось. Аналогичные факты имеют место и в случае, когда мера погрешности определяется интегральной метрикой, а также для функций многих переменных. Особую важность приобретает исследование скорости убывания числовой последовательности m (f, Р п(f)) в зависимости от свойств приближаемой функции и от выбора приближающих полиномов Р n(f, t). Наибольший интерес представляет изучение наилучшего приближения, а также приближения, доставляемого линейными методами, позволяющими но функции f(t) эффективно построить полином Pn(f, t). Важный этап в развитии теории П. ф., связанный с именами Ш. Ж. Балле Пуссена (Ch. J. La Vallee Poussin), Д. Джексона (D. Jackson), С. Н. Бернштейна, составили исследования связи между скоростью убывания погрешности приближения функции f(t) выбранными тем или иным способом многочленами Pn(f, t).степени п(при В 30-40-х гг. появились работы Л. Н. Колмогорова, Ж. Фавара (J. Favard) и С. М. Никольского, к-рые положили начало новому направлению исследований, связанному с приближением классов функций конечномерными подпространствами и получением точных оценок погрешности через задающие класс дифференциально-разностные характеристики. Речь идет об отыскании величин где m (g,j) - выбранная мера погрешности приближения, О некоторых других аспектах П. <ф. На приближающую функцию j(t)=j(f, t).из В прикладных задачах наряду с явно задаваемыми функциями возникает необходимость приближать кривые и поверхности, допускающие только параметрич. задание; в качестве аппарата приближения могут служить, напр., параметрич. сплайны. Меру погрешности здесь естественнее всего определить через хаусдорфово расстояние, к-рое хорошо учитывает геометрич. близость таких объектов, и, напр., для кривых l1 и l2 определяется равенством где r( Р, Q) -- евклидово (или какое-нибудь другое) расстояние между точками Ри Q. Хаусдорфово расстояние является более предпочтительным при выборе меры погрешности и в нек-рых ситуациях П. <ф., напр. когда разрывную функцию нужно аппроксимировать функцией гладкой (см. [16]). Решение ряда задач теории П. ф. тесно связано с исследованием экстремальных свойств полиномов по тем или иным конкретным системам функций (неравенства для производных многочленов, полиномы, наименее уклоняющиеся от нуля, и др.). В частности, доказательство обратных теорем П. ф. существенно базируется на неравенствах, дающих оценку нормы (или значения в фиксированной точке) нек-рой производной алгебраического или тригонометрич. полинома через те или иные характеристики самого полинома. В этом направлении известен ряд точных результатов, имеются обобщения на целые функции (см. [6] - [10]). Задача об алгебраич. многочлене (с фиксированным старшим коэффициентом), наименее уклоняющемся от нуля в метрике Сили Lp на отрезке [а, b], эквивалентная задаче о наилучшем приближении функции tn многочленами степени п-1, исследовалась П. Л. Чебышевым (метрика С).и его учениками (метрика L1). Решение дают многочлены Чебышева первого (С).и второго (L1) рода и многочлены Лежандра (L2), имеющие широкое применение как в теоретических, так и в прикладных исследованиях. Известен ряд результатов для более общего случая, когда на коэффициенты многочлена накладывается несколько связей (см. [6]). Задача о моносплайне минимальной нормы, эквивалентная отысканию наилучшего приближения функции tn сплайнами порядка п-1 со свободными узлами, приобрела особое значение в связи с тем, что к ней в ряде случаев сводится задача о наилучшей квадратурной формуле (см. [17]). О П. ф. в комплексной плоскости см. Приближение функций комплексного переменного. Лит.:[1] Чебышев П. Л., Вопросы о наименьших величинах, связанные с приближенным представлением функций (1859), Полн. собр. соч., т. 2, М.-Л., 1947, с. 151- 235; [2] Weierstrass К., "Sitzungsber. Akad. Berlin", 1885, S. 633- 639, 789-805; [3] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [4] Натансон И. П., Конструктивная теория функций, М.- Л., 1949; [5] Корнейчук Н. П., Экстремальные задачи теории приближения, М., 1976; [6] Дзядык В. К., Введение в теорию равномерного приближения функций полиномами, М., 1977; [7] Тихомиров В. М., Некоторые вопросы теории приближений, М., 1976; [8] Никольский С. М., Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977; [9] Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; [10] Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960; [11] Коровкин П. П., Линейные операторы и теория приближений, М., 1959; [12] Алберг Д ж., Нильсон Э., Уолш Д ж., Теория сплайнов и ее приложения, пер. с англ., М., 1972; [13] Стечкин С. Б., Субботин Ю. Н., Сплайны в вычислительной математике, М., 1976; [14] Лоран П. - Ж., Аппроксимация и оптимизация, пер. с франц., М., 1975; [15] Коллатц Л.,Крабе В., Теория приближений. Чебышевские приближения и их приложения, пер. с нем., М., 1978; [16] Сен до в Б., Хаусдорфовые приближения, София, 1979; [17] Никольский С. М., Квадратурные формулы, 3 изд., М., 1979; [18] Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л., Методы сплайн-функций, М., 1980; [19] Корнейчук Н. П., Лигун А. А., Доронин В. Г., Аппроксимация с ограничениями, К., 1982. Я. П. Корнейчук. |
|
|
|

 (приближающего множества). Предполагается, что функция f определена на том множестве Qm-мерного евклидова пространства (в частности, действительной оси), на к-ром осуществляется приближение, она может быть задана явно через элементарные функции или быть решением нек-рого уравнения. Если о функции f(t) располагают неполной информацией, то тогда речь идет, по существу, о приближении задаваемого этой информацией целого класса функций.
(приближающего множества). Предполагается, что функция f определена на том множестве Qm-мерного евклидова пространства (в частности, действительной оси), на к-ром осуществляется приближение, она может быть задана явно через элементарные функции или быть решением нек-рого уравнения. Если о функции f(t) располагают неполной информацией, то тогда речь идет, по существу, о приближении задаваемого этой информацией целого класса функций. ; выбор меры погрешности приближения; выбор метода приближения, т. е. правила, по к-рому функции f(t).сопоставляетcя функция j(t).из
; выбор меры погрешности приближения; выбор метода приближения, т. е. правила, по к-рому функции f(t).сопоставляетcя функция j(t).из  ; исследование и оценка, погрешности приближения.
; исследование и оценка, погрешности приближения. , помимо безусловного требования обеспечить нужную точность приближения, руководствуются стремлением иметь дело с простыми по структуре и удобными для вычисления функциями j(t), на к-рые могут накладываться априорные условия, связанные, напр., с гладкостью.
, помимо безусловного требования обеспечить нужную точность приближения, руководствуются стремлением иметь дело с простыми по структуре и удобными для вычисления функциями j(t), на к-рые могут накладываться априорные условия, связанные, напр., с гладкостью.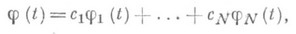
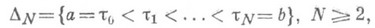 (1)
(1) Cr-k[a, b]и s(t).есть алгебраич. многочлен степени rна каждом промежутке (ti-1, ti), i=l, 2, ..., N. Напр., ломаная с узлами в точках ti есть сплайн первого порядка дефекта 1; непрерывно дифференцируемая на [а, b]функция s(t), совпадающая на [ti-1, ti],. i=1, ..., N, с кубич. многочленом, есть кубический сплайн дефекта 2 и т. д. Аналогично определяются сплайны двух и большего числа переменных. Имея конечную гладкость, сплайны обладают большей, чем полиномы, локальной гибкостью: изменение значений сплайна на нек-ром промежутке (a, b) мало сказывается (или совсем не сказывается) на поведении его вне (a, b). Преимущества сплайнов, помимо простоты машинной реализации, сказываются, в частности, там, где информация о приближаемой функции имеет дискретный характер, напр. значения в нек-рых точках самой функции f и, быть может, нек-рых ее производных.
Cr-k[a, b]и s(t).есть алгебраич. многочлен степени rна каждом промежутке (ti-1, ti), i=l, 2, ..., N. Напр., ломаная с узлами в точках ti есть сплайн первого порядка дефекта 1; непрерывно дифференцируемая на [а, b]функция s(t), совпадающая на [ti-1, ti],. i=1, ..., N, с кубич. многочленом, есть кубический сплайн дефекта 2 и т. д. Аналогично определяются сплайны двух и большего числа переменных. Имея конечную гладкость, сплайны обладают большей, чем полиномы, локальной гибкостью: изменение значений сплайна на нек-ром промежутке (a, b) мало сказывается (или совсем не сказывается) на поведении его вне (a, b). Преимущества сплайнов, помимо простоты машинной реализации, сказываются, в частности, там, где информация о приближаемой функции имеет дискретный характер, напр. значения в нек-рых точках самой функции f и, быть может, нек-рых ее производных.

 0 и рассматривают взвешенное приближение с мерой погрешности
0 и рассматривают взвешенное приближение с мерой погрешности 



 приближающую функцию j(t)=j(f, t) (при выборе метода приближения), естественно стремление обеспечить по возможности более высокую точность приближения и одновременно простоту построения j (f, t).по имеющейся информации о приближаемой функции f(t). Первое требование ориентирует на "ближайшую" к f(t) функцию jf(t) из
приближающую функцию j(t)=j(f, t) (при выборе метода приближения), естественно стремление обеспечить по возможности более высокую точность приближения и одновременно простоту построения j (f, t).по имеющейся информации о приближаемой функции f(t). Первое требование ориентирует на "ближайшую" к f(t) функцию jf(t) из  , т. е. такую, что
, т. е. такую, что 
 - замкнутое локально компактное множество, в частности конечномерное подпространство. Единственность зависит как от свойств приближающего множества
- замкнутое локально компактное множество, в частности конечномерное подпространство. Единственность зависит как от свойств приближающего множества  (см. Хаара условие, Чебяшева система функций), так и от метрики, определяющей меру погрешности m(f, j). Известен ряд необходимых и достаточных условий, к-рым должна удовлетворять функция наилучшего приближения jf(t).в той или иной ситуации (см. Наилучшего приближения многочлен, Чебышева теорема, Маркова критерий). Однако эти критерии, как правило, не дают способов эффективного построения функции jf(t). Поэтому большое значение имеют методы, к-рые позволяют по информации о приближаемой функции f(t).эффективно построить нек-рую функцию j(f, t).из
(см. Хаара условие, Чебяшева система функций), так и от метрики, определяющей меру погрешности m(f, j). Известен ряд необходимых и достаточных условий, к-рым должна удовлетворять функция наилучшего приближения jf(t).в той или иной ситуации (см. Наилучшего приближения многочлен, Чебышева теорема, Маркова критерий). Однако эти критерии, как правило, не дают способов эффективного построения функции jf(t). Поэтому большое значение имеют методы, к-рые позволяют по информации о приближаемой функции f(t).эффективно построить нек-рую функцию j(f, t).из  , обеспечивающую приемлемое приближение. Здесь, в первую очередь, надо говорить о линейных методах (когда
, обеспечивающую приемлемое приближение. Здесь, в первую очередь, надо говорить о линейных методах (когда  , к к-рым, в частности, относится метод интерполяции. Зафиксировав точки t1 . . ., tN из Q, можно выбирать j(f, t).среди тех функций j(t).из
, к к-рым, в частности, относится метод интерполяции. Зафиксировав точки t1 . . ., tN из Q, можно выбирать j(f, t).среди тех функций j(t).из  , к-рые удовлетворяют условию интерполяции
, к-рые удовлетворяют условию интерполяции  (2)
(2) - линейное многообразие и в нем существует система функции j1; . . ., jN такая, что ji(ti)=1, ji(tk)=0 (k
- линейное многообразие и в нем существует система функции j1; . . ., jN такая, что ji(ti)=1, ji(tk)=0 (k i) , то функция
i) , то функция 
 и удовлетворяет условиям (2); она задает интерполяционный метод приближения, являющийся, очевидно, линейным. Функцию j(f, t).можно выбирать, требуя совпадения в точках tk не только f(t).и j(f, t), но и нек-рых их производных; в этом случае говорят об интерполировании с кратными узлами. Если
и удовлетворяет условиям (2); она задает интерполяционный метод приближения, являющийся, очевидно, линейным. Функцию j(f, t).можно выбирать, требуя совпадения в точках tk не только f(t).и j(f, t), но и нек-рых их производных; в этом случае говорят об интерполировании с кратными узлами. Если  , то существует единственный алгебраич. многочлен степени N-1, а в непериодич. случае (b- а=2p, tN=t2n-1<b) - единственный тригонометрич. полином порядка п-1, совпадающий с f(t).в точках tk. Кратное интерполирование осуществляют интерполяционные полиномы Эрмита, частным случаем к-рых является многочлен Тейлора, когда в одной точке алгебраич. многочленом степени пинтерполируются значения функции и ее первых ппроизводных.
, то существует единственный алгебраич. многочлен степени N-1, а в непериодич. случае (b- а=2p, tN=t2n-1<b) - единственный тригонометрич. полином порядка п-1, совпадающий с f(t).в точках tk. Кратное интерполирование осуществляют интерполяционные полиномы Эрмита, частным случаем к-рых является многочлен Тейлора, когда в одной точке алгебраич. многочленом степени пинтерполируются значения функции и ее первых ппроизводных. дефекта 1 по разбиению (1), принимающий заданные значения в Nразличных точках ti интервала ( а, b).таких, что
дефекта 1 по разбиению (1), принимающий заданные значения в Nразличных точках ti интервала ( а, b).таких, что  , i=1, 2, . . ., N, существует и единствен, если задать определенным образом краевые условия в виде т а чисел
, i=1, 2, . . ., N, существует и единствен, если задать определенным образом краевые условия в виде т а чисел  и т b чисел
и т b чисел  , причем ma+mb=r. Функции
, причем ma+mb=r. Функции  можно однозначно сопоставить сплайн s(f, t).порядка 2r-1 дефекта
можно однозначно сопоставить сплайн s(f, t).порядка 2r-1 дефекта  по разбиению (1), потребовав выполнения равенств
по разбиению (1), потребовав выполнения равенств  , v=0, 1, ..., k-1; i=0, 1, . . ., N, а при k<r -также нек-рых краевых условий. При k=r этот сплайн иаз. эрмитовым, а также локальным, т. <к. его поведение на интервале
, v=0, 1, ..., k-1; i=0, 1, . . ., N, а при k<r -также нек-рых краевых условий. При k=r этот сплайн иаз. эрмитовым, а также локальным, т. <к. его поведение на интервале  определяется только значениями функции f(t).и ее производных f(v)(t).(v=l, . . ., k-1) в точках ti-1 и ti.
определяется только значениями функции f(t).и ее производных f(v)(t).(v=l, . . ., k-1) в точках ti-1 и ti.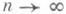
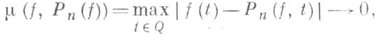
 ) и дифференциально-разностными свойствами f(t). Оказалось, что эти свойства, т. е. наличие у f(t).производных, их гладкость и т. д., можно в ряде случаев охарактеризовать через последовательность приближающих полиномов и поведение доставляемой ими погрешности (см. Приближение функций;прямые и обратные теоремы). Этим давалась новая, конструктивная характеристика непрерывных и дифференцируемых функций. В первой трети 20 в. такая проблематика была доминирующей в теории приближения, что дало повод говорить о ней как о конструктивной теории функций.
) и дифференциально-разностными свойствами f(t). Оказалось, что эти свойства, т. е. наличие у f(t).производных, их гладкость и т. д., можно в ряде случаев охарактеризовать через последовательность приближающих полиномов и поведение доставляемой ими погрешности (см. Приближение функций;прямые и обратные теоремы). Этим давалась новая, конструктивная характеристика непрерывных и дифференцируемых функций. В первой трети 20 в. такая проблематика была доминирующей в теории приближения, что дало повод говорить о ней как о конструктивной теории функций.
 - нек-рый класс функций, a PN(f, t).- приближающий (вообще говоря, обобщенный) полином, коэффициенты к-рого определяются выбором метода приближения. Результаты такого рода позволяют сравнивать методы приближения с точки зрения их аппроксимативных возможностей и ставить важную для приложений задачу отыскания для данного класса функций оптимального (наилучшего) приближающего аппарата (фиксированной размерности N). Исследования в этом направлении, базирующиеся как на изучении свойств конкретных методов приближения, так и на самых общих положениях функционального анализа, оказались весьма плодотворными и в идейном отношении, т. к. привели к установлению принципиально новых фактов о связи между различными по характеру экстремальными задачами, позволили выявить глубокие и тонкие зависимости в теории функций. Благодаря этому оказалось возможным до конца решить ряд экстремальных задач по наилучшему приближению важнейших классов функций (см. [5], [7], а также Приближение функций;экстремальные задачи на классах функций).
- нек-рый класс функций, a PN(f, t).- приближающий (вообще говоря, обобщенный) полином, коэффициенты к-рого определяются выбором метода приближения. Результаты такого рода позволяют сравнивать методы приближения с точки зрения их аппроксимативных возможностей и ставить важную для приложений задачу отыскания для данного класса функций оптимального (наилучшего) приближающего аппарата (фиксированной размерности N). Исследования в этом направлении, базирующиеся как на изучении свойств конкретных методов приближения, так и на самых общих положениях функционального анализа, оказались весьма плодотворными и в идейном отношении, т. к. привели к установлению принципиально новых фактов о связи между различными по характеру экстремальными задачами, позволили выявить глубокие и тонкие зависимости в теории функций. Благодаря этому оказалось возможным до конца решить ряд экстремальных задач по наилучшему приближению важнейших классов функций (см. [5], [7], а также Приближение функций;экстремальные задачи на классах функций). могут накладываться дополнительные ограничения. Если они не связаны с функцией f (напр., ограничения или связи на коэффициенты приближающего полинома), то дело фактически сводится к уточнению приближающего множества
могут накладываться дополнительные ограничения. Если они не связаны с функцией f (напр., ограничения или связи на коэффициенты приближающего полинома), то дело фактически сводится к уточнению приближающего множества  . Новая ситуация возникает, если ограничения на j(f, t).связаны с приближаемой функцией f; один из интересных случаев - одностороннее приближение, когда j(f, t).из
. Новая ситуация возникает, если ограничения на j(f, t).связаны с приближаемой функцией f; один из интересных случаев - одностороннее приближение, когда j(f, t).из  должна удовлетворять неравенству
должна удовлетворять неравенству  (или
(или  ) и погрешность оценивается в интегральной метрике (см. [19]).
) и погрешность оценивается в интегральной метрике (см. [19]).