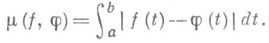" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ПРИБЛИЖЕНИЕ В СРЕДНЕМ

Значение ПРИБЛИЖЕНИЕ В СРЕДНЕМ в математической энциклопедии:

приближение заданной и интегрируемой на промежутке [ а, b]функции f(t). функцией j(t), когда за меру погрешности принята величина

В более общем случае, когда

где s(t) - неубывающая на [ а, b]отличная от постоянной функция, говорят о сроднестепенном (с показателем q).приближении относительно распределения ds(t). Если s(t).абсолютно непрерывна и р(t)=s'(t), получают среднестепенное приближение с весом r(t), если же s(t) - ступенчатая функция со скачками c_k в точках t_k из [а, b], то приходят к взвешенному среднестепенному приближению в системе точек {t_k} с мерой погрешности

Естественным образом эти понятия обобщаются на случай функций многих переменных.

Лит.:[1] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [2] Никольский С. М., Приближение функций многих переменных и теоремы вложения, 2 изд., М., 1977.

Н. П. Корнейчук, В. П. Моторный.