|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПРЕДСТАВИМЫЙ ФУНКТОРЗначение ПРЕДСТАВИМЫЙ ФУНКТОР в математической энциклопедии: ковариантный (или контравариантный) функтор Fиз нек-рой категории Функтор В категории множеств тождественный функтор представим: представляющим объектом служит одноточечное множество. Функтор взятия нек-рой декартовой степени также представим: представляющим объектом служит множество, мощность к-рого равна этой степени. В произвольной категории произведение П. ф. Fi с представляющими объектами П. ф.- аналог понятия "свободная универсальная алгебра с одним образующим". Для любого функтора Для аддитивных категорий вместо функторов со значениями в Понятие П. ф. первоначально возникло в алгебраич. геометрии (см. [2]). Наиболее важными примерами П. ф. здесь являются функторы Пикара Pic X/S и Гильберта Hilb X/S, представимые в категории алгебраических пространств (см. [1]). Пусть К - поле частных регулярного дискретного нормированного кольца О с совершенным полем вычетов. Если Х 0- гладкая геометрически неприводимая собственная кривая рода g>0 над К, то ее минимальная модель представляет функтор Лит.:[1] Артин М., "Математика", 1970. т. 14, М 4, с. 3-39; [2] Гротендик А., Дьёдонно Ж., "Успехи матем. наук", 1972, т. 27, в. 2, с. 135-48. С. Г. Танкеев, М. Ш. Цаленко. |
|
|
|

 в категорию множеств
в категорию множеств 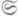 , изоморфный одному из основных теоретико-множественных функторов:
, изоморфный одному из основных теоретико-множественных функторов:
 представим тогда и только тогда, когда найдутся такие объект
представим тогда и только тогда, когда найдутся такие объект  и элемент
и элемент  , что для каждого элемента
, что для каждого элемента  , существует единственный морфизм
, существует единственный морфизм  , для к-рого x=aF(a). Объект Аназывается представляющим функтор F;он определен однозначно с точностью до изоморфизма.
, для к-рого x=aF(a). Объект Аназывается представляющим функтор F;он определен однозначно с точностью до изоморфизма. , представимо тогда и только тогда, когда в этой категории существует копроизведение объектов Ai. Всякий ковариантный П. ф. перестановочен с пределами, т, е. непрерывен.
, представимо тогда и только тогда, когда в этой категории существует копроизведение объектов Ai. Всякий ковариантный П. ф. перестановочен с пределами, т, е. непрерывен. и П. ф. Fмножество естественных преобразований Nat(F, G) изоморфно множеству G(A), где А - представляющий объект. Это показывает, что П. ф. являются свободными объектами категории функторов.
и П. ф. Fмножество естественных преобразований Nat(F, G) изоморфно множеству G(A), где А - представляющий объект. Это показывает, что П. ф. являются свободными объектами категории функторов. рассматриваются аддитивные функторы со значениями в категории абелевых групп; поэтому под П. ф. понимается аддитивный функтор, изоморфный основному аддитивному функтору.
рассматриваются аддитивные функторы со значениями в категории абелевых групп; поэтому под П. ф. понимается аддитивный функтор, изоморфный основному аддитивному функтору. из категории регулярных O-схем. Если А - абелево многообразие над К, то его минимальная Нерона модель является гладкой групповой схемой
из категории регулярных O-схем. Если А - абелево многообразие над К, то его минимальная Нерона модель является гладкой групповой схемой 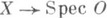 , представляющей функтор
, представляющей функтор  из категории гладких О-схем.
из категории гладких О-схем.