Математический словарь
" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

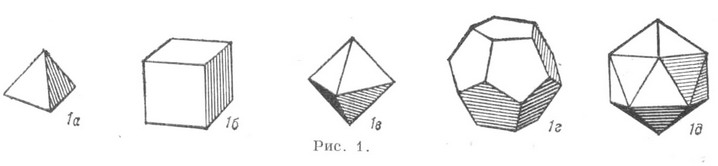
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Значение ПРАВИЛЬНЫЕ МНОГОГРАННИКИ в математической энциклопедии:

тела Платона,- выпуклые многогранники, все грани к-рых


суть одинаковые правильные многоугольники и все многогранные углы при вершинах правильные и равные (рис. 1a-1д).

В евклидовом пространстве Е 3 существуют пять П. м., данные о к-рых приведены в табл. 1, где символ Шлефли {р, q} (см. Многогранника группа).обозначает П. м. с p-угольными гранями и q-гранными углами.

Табл. 1. -Правильные (выпуклые) многогранники в Е 3

Рис.

Символ Шлефли

Число вершин

Число ребер

Число граней

Тетраэдр

1а

{3,3}

4

6

4

Куб (гексаэдр)

16

{4,3}

8

12

6

Октаэдр

1в

{3,4}

6

12

8

Додекаэдр

1г

{5,3}

20

30

12

Икосаэдр

1д

{3,5}

12

30

20

Двойственными многогранниками {р, q} и {q, p} наз. такие, к-рые переходят друг в друга при полярном преобразовании относительно вписанной

Табл. 2.-Правильные многогранники в Е 4

Символ Шлефли

Число вершин

Число ребер

Число двумерных граней

Число трехмерных граней

Симплекс

{3, 3, 3}

5

10

10

5

Гиперкуб

{4, 3, 3}

16

32

24

8

16-гранник

{3, 3, 4}

8

24

32

16

24-гранник

{3, 4, 3}

24

96

96

24

120-гранник

{5, 3, 3}

600

1200

720

120

600-гранник

{3, 3, 5}

120

720

1200

600

или описанной сферы. Тетраэдр двойствен сам себе, гексаэдр - октаэдру и додекаэдр - икосаэдру.

В пространстве E4 существуют шесть П. м., данные о к-рых приведены в табл. 2.

В пространстве Е n, n>4, существует три П. м.- аналоги тетраэдра, октаэдра и куба; их символы Шлеф-ли- {3, ... ,3}, {4,3, ... ,3}, {3, ... ,3, 4}.

Если под многоугольником понимать плоские замкнутые ломаные (хотя бы и самопересекающиеся), то можно указать еще 4 невыпуклых (звездчатых) П. м. (тела Пуансо).

В этих многогранниках либо грани пересекают друг друга, либо грани - самопересекающиеся многоугольники (рис. 2а-2г). Данные о них приведены в табл. 3.

Табл. 3.-П р а в и л ь н ы е (невыпуклые) многогранники в Е 3

Рис.

Число вершин

Число ребер

Число граней

Малый звездчатый додекаэдр

2а

12

30

12

Большой звездчатый додекаэдр

2б

20

30

12

Большой додекаэдр

2в

12

30

12

Икосаэдр

2г

12

30

20

Лит.:[1] Энциклопедия элементарной математики, кн. 4- Геометрия, М., 196IJ; 12] Люстерник Л. А., Выпуклые фигуры и многогранники, М., 1956; [3] Шклярский Д. О., Ченцов Н. Н., Яглом И. М., Избранные задачи и теоремы элементарной математики, ч. 3, М., 1954; [4] Соxeter Н. S. М., Regular polytopes, 3 ed., N.Y., 1973.

А. Б. Иванов.