|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОТЕНЦИАЛОВ МЕТОДЗначение ПОТЕНЦИАЛОВ МЕТОД в математической энциклопедии: - метод исследования краевых задач для уравнений математич. физики путем сведения их к интегральным уравнениям, основанный на представлении решений этих задач в виде (обобщенных) потенциалов. Пусть в пространстве с достаточно гладкими коэффициентами а ij=а ji=aij(x). ei=ei(x), c(x) где S=дD - граница области D, Е( х, у) - главное фундаментальное решение оператора L, символ Qy обозначает оператор действующий в точке v - единичный вектор внешней нормали к Sв точке Для потенциалов (2) - (4) остаются в силе, с соответствующими изменениями, все дифференциальные и граничные свойства гармонич. потенциалов, описанные в ст. Потенциала теория для случая, когда L - оператор Лапласа. На основании этих свойств удается свести краевые задачи для эллиптич. уравнений типа (1) к интегральным уравнениям, аналогично тому, как это было описано для задач Дирихле и Неймана для гармонич. функций в ст. Потенциала теория. Лит.:[1] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [2] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [3] Владимиров В. С., Уравнения математической физики, 4 изд., М.,. 1981; [4] Купрадзе В. Д., Методы потенциала в теории упругости, М., 1903; [5] Милн - Томсон Л. М., Теоретическая гидродинамика, пер. с англ., М., 1964. Е. Д. Соломенцев. |
|
|
|

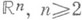 , задано дифференциальное
, задано дифференциальное 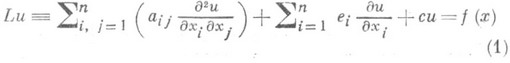
 0 и правой частью f(x), причем с(x)<-k2<0 вне нек-рой ограниченной области, содержащей внутри область Dкласса C1. Тогда любое решение и(х).уравнения (1) класса
0 и правой частью f(x), причем с(x)<-k2<0 вне нек-рой ограниченной области, содержащей внутри область Dкласса C1. Тогда любое решение и(х).уравнения (1) класса 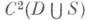 можно представить в виде суммы трех (обобщенных) потенциалов: потенциала объемных масс
можно представить в виде суммы трех (обобщенных) потенциалов: потенциала объемных масс 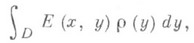 (2) потенциала простого слоя
(2) потенциала простого слоя 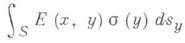 (3) и потенциала двойного слоя
(3) и потенциала двойного слоя 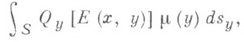 (4)
(4)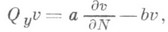
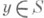 , N - единичный вектор конормали в точке
, N - единичный вектор конормали в точке 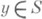 ,
,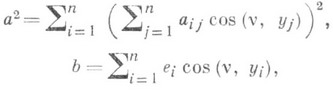
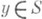 . Плотности потенциалов r(y), s(у).и m(у) - достаточно гладкие функции на Dили S.
. Плотности потенциалов r(y), s(у).и m(у) - достаточно гладкие функции на Dили S.