Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕРНУЛЛИ УРАВНЕНИЕЗначение БЕРНУЛЛИ УРАВНЕНИЕ в математической энциклопедии: - обыкновенное дифференциальное уравнение 1-го порядка где. также есть Б. у., если рассматривать укак независимую переменную, а х - как неизвестную функцию от у. Лит.:[1] Bernoulli J., "Acta Erud.", 1695, p. 59-67, 537-57; [2] Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976. Н. X. Розов. |
|
|
|


 - действительное число, не равное нулю и единице. Это уравнение впервые было рассмотрено Я. Бернулли [1]. Подстановкой
- действительное число, не равное нулю и единице. Это уравнение впервые было рассмотрено Я. Бернулли [1]. Подстановкой  Б. у. приводится к линейному неоднородному уравнению 1-го порядка (см. [2]). Если
Б. у. приводится к линейному неоднородному уравнению 1-го порядка (см. [2]). Если 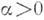 , то Б. у. имеет решение
, то Б. у. имеет решение  ; при
; при  в точках этого решения нарушается единственность. Уравнение вида
в точках этого решения нарушается единственность. Уравнение вида 