|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОСЛЕДОВАТЕЛЬНОСТЬЗначение ПОСЛЕДОВАТЕЛЬНОСТЬ в математической энциклопедии: элементов заданного множества - функция, определенная на множестве натуральных чисел, множество значений к-рой содержится в рассматриваемом множестве. Элементом, или членом, последовательности Множество элементов П. всегда счетно, причем два различных члена П. отличаются по крайней мере номерами. Множество значений элементов П. может быть и конечным; так, множество значений всякой стационарной П., т. е. последовательности {xn}, все элементы к-рой имеют одно и то же значение: х п=а, n=1, 2, . . ., состоит из одного элемента. Если n1<n2, то член xn1 последовательности {х п} наз. предшествующим члену х п2, а член х п2 - следующим за членом xn1. Таким образом, множество элементов П. упорядочено. Того или иного рода П. встречаются в различных разделах математики и с их помощью описываются многие свойства изучаемых объектов. Напр., если X - топологич. пространство, то среди П. его точек важную роль играют сходящиеся П., т. е. П., к-рые имеют предел в этих пространствах. В терминах сходящихся П. удобно (во всяком случае, при наличии счетной базы) описывать свойство компактности, существование предела отображения, его непрерывность и т. п. Если все элементы П. нек-рых объектов (точек, множеств, отображений и т. д.) обладают каким-либо свойством, то часто бывает нужным выяснить, сохраняется ли это свойство для предела П.; напр., выяснить, как ведут себя свойства измеримости, непрерывности, дифференцируемости, интегрируемости при предельном переходе для различных видов сходимости функций (поточечной, почти всюду, равномерной, по мере, в среднем и т. п.). Иногда отображение |
|
|
|

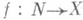 , где N - множество натуральных чисел, X - заданное множество, наз. упорядоченная пара
, где N - множество натуральных чисел, X - заданное множество, наз. упорядоченная пара  , к-рая обозначается через х n. Натуральное число n наз. номером элемента последовательности х п, а элемент
, к-рая обозначается через х n. Натуральное число n наз. номером элемента последовательности х п, а элемент  - его значением. Последовательность
- его значением. Последовательность  обычно обозначается через {х п} или х п, п= 1, 2, ....
обычно обозначается через {х п} или х п, п= 1, 2, .... конечного множества
конечного множества  натуральных чисел в множество Xназ. конечной П. и обозначается через { х 1, х 2, . .., х п}, где xn=f(k), k=1, 2, . . ., п. П. может задаваться формулой ее общего члена (напр., П. членов арифметич. прогрессии), рекуррентной формулой (напр., П. чисел Бернулли) или просто словесным описанием с той или иной степенью эффективности (напр., П. всех простых натуральных чисел в порядке их возрастания). См. также Двойная последовательность, Кратная последовательность. Обобщением понятия П. является направленность. Л. Д. Кудрявцев.
натуральных чисел в множество Xназ. конечной П. и обозначается через { х 1, х 2, . .., х п}, где xn=f(k), k=1, 2, . . ., п. П. может задаваться формулой ее общего члена (напр., П. членов арифметич. прогрессии), рекуррентной формулой (напр., П. чисел Бернулли) или просто словесным описанием с той или иной степенью эффективности (напр., П. всех простых натуральных чисел в порядке их возрастания). См. также Двойная последовательность, Кратная последовательность. Обобщением понятия П. является направленность. Л. Д. Кудрявцев.