"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОСЛЕДОВАТЕЛЬНОСТЕЙ КАТЕГОРИЯ
Значение ПОСЛЕДОВАТЕЛЬНОСТЕЙ КАТЕГОРИЯ в математической энциклопедии:
частный случай общей конструкции категории функторов или категории диаграмм. Пусть  - множество целых чисел, снабженное обычным отношением порядка. Тогда
- множество целых чисел, снабженное обычным отношением порядка. Тогда  можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где
можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где  и
и  Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k).
Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k).
Для произвольной категории  категория кова-риантных функторов
категория кова-риантных функторов  из
из  в
в 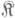 наз. категорией последовательностей над
наз. категорией последовательностей над  Чтобы задать функтор
Чтобы задать функтор  , достаточно указать семейство объектов из
, достаточно указать семейство объектов из  , заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм
, заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм  Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора
Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора  . Естественное преобразование j функтора
. Естественное преобразование j функтора  в функтор
в функтор  , т. е. морфизм категории последовательностей, задается таким семейством морфизмов
, т. е. морфизм категории последовательностей, задается таким семейством морфизмов  , что jiG(i,i+1)=F(i,i+1).ji+1 для любого
, что jiG(i,i+1)=F(i,i+1).ji+1 для любого  .
.
Если 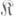 - категория с нулевыми морфизмами, то в П. к.
- категория с нулевыми морфизмами, то в П. к.  выделяется полная подкатегория комплексов, т. е. таких функторов
выделяется полная подкатегория комплексов, т. е. таких функторов  , что F(i, i+1) F(i+1, i+2) = 0 для любого
, что F(i, i+1) F(i+1, i+2) = 0 для любого  . Для абелевой категории
. Для абелевой категории  П. к. и подкатегория комплексов являются абелевыми категориями.
П. к. и подкатегория комплексов являются абелевыми категориями.
Вместо категории  можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.
можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.

 - множество целых чисел, снабженное обычным отношением порядка. Тогда
- множество целых чисел, снабженное обычным отношением порядка. Тогда  можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где
можно рассматривать как малую категорию, объектами к-рой являются целые числа, а морфизмами - всевозможные пары вида (i, j), где  и
и  Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k).
Пара (i, j) - это единственный морфизм объекта iв объект j. Композиция морфизмов определяется следующим равенством: (i, j)(j, k)=(i, k). категория кова-риантных функторов
категория кова-риантных функторов  из
из  в
в 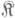 наз. категорией последовательностей над
наз. категорией последовательностей над  Чтобы задать функтор
Чтобы задать функтор  , достаточно указать семейство объектов из
, достаточно указать семейство объектов из  , заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм
, заиндексированное целыми числами, и для каждой пары объектов А i, Ai+1 выбрать произвольный морфизм  Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора
Тогда отображения F(i)=Ai,F(i,i+1)=ai,i+1 однозначно продолжаются до функтора  . Естественное преобразование j функтора
. Естественное преобразование j функтора  в функтор
в функтор  , т. е. морфизм категории последовательностей, задается таким семейством морфизмов
, т. е. морфизм категории последовательностей, задается таким семейством морфизмов  , что jiG(i,i+1)=F(i,i+1).ji+1 для любого
, что jiG(i,i+1)=F(i,i+1).ji+1 для любого  .
.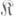 - категория с нулевыми морфизмами, то в П. к.
- категория с нулевыми морфизмами, то в П. к.  выделяется полная подкатегория комплексов, т. е. таких функторов
выделяется полная подкатегория комплексов, т. е. таких функторов  , что F(i, i+1) F(i+1, i+2) = 0 для любого
, что F(i, i+1) F(i+1, i+2) = 0 для любого  . Для абелевой категории
. Для абелевой категории  П. к. и подкатегория комплексов являются абелевыми категориями.
П. к. и подкатегория комплексов являются абелевыми категориями. можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.
можно рассматривать ее подкатегории, состоящие только из неотрицательных или только из неположительных чисел. Соответствующие категории диаграмм также наз. П. к. М. Ш. Цаленко.