|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛУТОРАЛИНЕЙНАЯ ФОРМАЗначение ПОЛУТОРАЛИНЕЙНАЯ ФОРМА в математической энциклопедии: - функция от двух переменных на модуле (напр., на векторном пространстве), линейная но одному переменному и полулинейная по другому. Точнее, П. ф, на унитарном модуле Енад ассоциативно-коммутативным кольцом А с единицей, снабженным автоморфизмом II. ф. можно рассматривать и на модулях над некоммутативным кольцом А;в этом случае предполагается, что а - антиавтоморфизм, т. е. что Для П. ф. удается ввести многие понятия теории билинейных форм, напр. понятия ортогонального подмодуля, левого и правого ядра, невырожденной формы, матрицы формы в данном базисе, ранга формы, сопряженных гомоморфизмов. Лит.: [1] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1986; [2] Ленг С., Алгебра, пер. с англ., М., 1968. А. Л. Онищик. |
|
|
|

 , наз. отображение
, наз. отображение  , линейное при фиксированном втором аргументе и полулинейное (см. Полулинейное отображение).при фиксированном первом аргументе. Аналогично определяется полуторалинейное отображение
, линейное при фиксированном втором аргументе и полулинейное (см. Полулинейное отображение).при фиксированном первом аргументе. Аналогично определяется полуторалинейное отображение 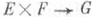 , где Е, F, G-А- модули. В случае, когда
, где Е, F, G-А- модули. В случае, когда  , получается понятие билинейной формы (и билинейного отображения). Другой важный пример П. ф. получается, когда V - векторное пространство над полем С и
, получается понятие билинейной формы (и билинейного отображения). Другой важный пример П. ф. получается, когда V - векторное пространство над полем С и  Специальным случаем П. ф. являются эрмитовы формы (а также косо-эрмитовы формы).
Специальным случаем П. ф. являются эрмитовы формы (а также косо-эрмитовы формы).