" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ПОЛУСИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО

Значение ПОЛУСИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО в математической энциклопедии:

проективное (2n+1)-пространство, в к-ром, задана (2n- 2m₀-1 )-плоскость Т ₀, в ней - (2n-2т ₁ - 1 )-плоскость T₁ и т. д. до (2n-2m_r-1-1 )-плоскости T_r-1, при этом в пространстве задана нуль-система, переводящая все точки пространства в плоскости, проходящие через плоскость T₀; в плоскости Т ₀ задана абсолютная нульсистема, переводящая все ее точки в (2n-2m₀-2)-плоскости, лежащие в ней и проходящие через (2n-2m_l-1 )-плоскость T₁ и т. д. до абсолютной нульсистемы (2n-2m_r-1-1)-плоскостп T_r-1, переводящей все ее точки в (2п-2m_r-1-2)-плоскости, лежащие в ней, .

П. п. обозначается

.

П. п. получается методом, аналогичным переходу от эллиптич. и гиперболич. пространств к полуэллиптич. и полугиперболич. пространствам, и является более общим по отношению к квазисимплектич. пространству.

Коллинеации П. п., переводящие в себя плоскости T_i, перестановочные с нуль-системами, наз. полусимплектическими преобразованиями П. п.

Существуют инварианты полусимплектич. преобразований, аналогичные симнлектич. инварианту симплектич. пространств. Полусимнлектич. преобразования образуют группу, являющуюся группой Ли.

Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Л. А. Сидоров.
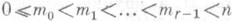