"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛУПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВОЗначение ПОЛУПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО в математической энциклопедии:
векторное пространство с вырожденной индефинитной метрикой. П. п.  определяется как n-мерное пространство, в к-ром задано rскалярных произведений определяется как n-мерное пространство, в к-ром задано rскалярных произведений  где 0=m0<m1<. . .<mr=n; a=l, 2, ..,, r; ia=ma-1+ + 1, ..., ma, где 0=m0<m1<. . .<mr=n; a=l, 2, ..,, r; ia=ma-1+ + 1, ..., ma,  =+1, причем - 1 среди чисел =+1, причем - 1 среди чисел  встречается la раз. Произведение (x, y) а определено для тех векторов, для к-рых все координаты х' при i встречается la раз. Произведение (x, y) а определено для тех векторов, для к-рых все координаты х' при i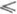 m а_1 равны нулю. На этих векторах справедливо равенство ( х, y)a-1=0. Первый скалярный квадрат произвольного вектора хП. п. является вырожденной квадратичной формой от координат вектора: m а_1 равны нулю. На этих векторах справедливо равенство ( х, y)a-1=0. Первый скалярный квадрат произвольного вектора хП. п. является вырожденной квадратичной формой от координат вектора:

где I - индекс, d=n-т 1 - дефект П. п. При l1=l2==:.. = ir=0 п. п. является полуевклидовым, пространством. В П. п. определяются m-мерные плоскости (m<n), прямые, параллельность, длина вектора так же, как в, псевдоевклидовых пространствах. В П. п.  можно выбрать ортогональный базис, состоящий из ,l векторов мнимой длины, п-l-dвещественной длинш и dизотропных векторов. Через каждую точку П; п. дефекта dможно провести d-мерную изотропную плоскость, каждый вектор к-рой ортогонален всем векторам П. <п. См. также Галилеево пространство. Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Д. Д. Соколов. можно выбрать ортогональный базис, состоящий из ,l векторов мнимой длины, п-l-dвещественной длинш и dизотропных векторов. Через каждую точку П; п. дефекта dможно провести d-мерную изотропную плоскость, каждый вектор к-рой ортогонален всем векторам П. <п. См. также Галилеево пространство. Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Д. Д. Соколов.
|

 определяется как n-мерное пространство, в к-ром задано rскалярных произведений
определяется как n-мерное пространство, в к-ром задано rскалярных произведений  где 0=m0<m1<. . .<mr=n; a=l, 2, ..,, r; ia=ma-1+ + 1, ..., ma,
где 0=m0<m1<. . .<mr=n; a=l, 2, ..,, r; ia=ma-1+ + 1, ..., ma,  =+1, причем - 1 среди чисел
=+1, причем - 1 среди чисел  встречается la раз. Произведение (x, y) а определено для тех векторов, для к-рых все координаты х' при i
встречается la раз. Произведение (x, y) а определено для тех векторов, для к-рых все координаты х' при i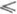 m а_1 равны нулю. На этих векторах справедливо равенство ( х, y)a-1=0. Первый скалярный квадрат произвольного вектора хП. п. является вырожденной квадратичной формой от координат вектора:
m а_1 равны нулю. На этих векторах справедливо равенство ( х, y)a-1=0. Первый скалярный квадрат произвольного вектора хП. п. является вырожденной квадратичной формой от координат вектора:
 можно выбрать ортогональный базис, состоящий из ,l векторов мнимой длины, п-l-dвещественной длинш и dизотропных векторов. Через каждую точку П; п. дефекта dможно провести d-мерную изотропную плоскость, каждый вектор к-рой ортогонален всем векторам П. <п. См. также Галилеево пространство. Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Д. Д. Соколов.
можно выбрать ортогональный базис, состоящий из ,l векторов мнимой длины, п-l-dвещественной длинш и dизотропных векторов. Через каждую точку П; п. дефекта dможно провести d-мерную изотропную плоскость, каждый вектор к-рой ортогонален всем векторам П. <п. См. также Галилеево пространство. Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Д. Д. Соколов.