|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛУНЕПРЕРЫВНЫЙ МЕТОД СУММИРОВАНИЯЗначение ПОЛУНЕПРЕРЫВНЫЙ МЕТОД СУММИРОВАНИЯ в математической энциклопедии: - метод суммирования рядов и последовательностей, определенный с помощью последовательности функций. Пусть {аk(w)}, k=0, 1, ... ,- последовательность функций, заданных на нек-ром множестве Еизменения параметра w, и w0 - точка сгущения этого множества (конечная или бесконечная). Данную последовательность {sn} с помощью функций а k(w) преобразуют в функцию s(w): Если ряд в (1) сходится для всех со, достаточно близких к w0, и то последовательность {sn} наз. суммируемой к пределу s полунепрерывным методом суммирования, определенным последовательностью функций {ak(w)}. Если {sn} - последовательность частичных сумм ряда то ряд (2) в этом случае наз. суммируемым полунепрерывным методом к сумме s. П. м. с. при w0= П. м. с. может задаваться преобразованием непосредственно ряда в функцию с помощью заданной последовательности функций, напр, {gk(w)}: В этом случае ряд (2) наз. суммируемым к сумме s, если где w0 - точка сгущения множества Еизменения параметра w, а ряд в (3)предполагается сходящимся для всех w, достаточно близких к w0. П. м. с. в нек-рых случаях являются более удобными, чем методы суммирования, определенные обычными матрицами, т. к. позволяют использовать аппарат теории функций. Примерами П. м. с. являются Абеля метод суммирования, Бореля метод суммирования, Линделёфа метод суммирования, Миттаг-Леффлера метод суммирования. Класс П. м. с. составляют методы с полунепрерывными матрицами вида где в знаменателе стоит целая функция, не сводящаяся к многочлену. Условия регулярности П. м. с. аналогичны условиям регулярности матричного метода суммирования. Напр., условия
для всех со, достаточно близких к w0, являются необходимыми и достаточными, чтобы П. м. с., определенный преобразованием (1) последовательности {sk} в функцию, был регулярным (см. Регулярности признаки). Лит.:[1] Xарди Г., Расходящиеся ряды, пер. с англ., М., 1951; [2] Кук Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., J960; [3] Zеllеr К., Bukmann W., Theorie der Limitierungsverfahren, 2 Aufl., В. -Hdlb. -N.Y., 1970. И. <И. <Волков. |
|
|
|
(1)
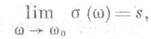
(2)
является аналогом матричного метода суммирования, определенного матрицей || а nk||, причем целочисленный параметр пзаменен непрерывным параметром w. Последовательность функций ak(w).в этом случае наз. полунепрерывной матрицей.
(3)
