|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛУМАРКОВСКИЙ ПРОЦЕССЗначение ПОЛУМАРКОВСКИЙ ПРОЦЕСС в математической энциклопедии: случайный процесс X(t)с конечным или счетным множеством состояний N={l, 2, ...}, имеющий ступенчатые траектории со скачками в моменты времени 0<t1<t2<... . Значения П. п. X(tn) в моменты скачков образуют Маркова цепь с переходными вероятностями Распределения моментов скачков tn описываются с помощью функций распределения Fij(x).следующим образом: (и при этом не зависят от состояний процесса в более ранние моменты времени). Если для всех П. п. служит моделью многих процессов массового обслуживания и теории надежности. С П. п. связаны процессы марковского восстановления (см. Восстановления теория), описывающие количество посещений процессом X(t).состояний Изучение П. п. и марковских процессов восстановления аналитически сводится к системе интегральных уравнений восстановления. Лит.:[1] Королюк В. С., Турбин А. Ф., Полумарковские процессы и их приложения, К., 1970. Б. А. Севастьянов. |
|
|
|

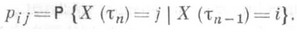
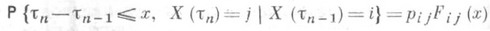
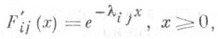
 , то П. п. X(t).является цепью Маркова с непрерывным временем. Если все распределения вырождены в одной точке, то получают цепь Маркова с дискретным временем.
, то П. п. X(t).является цепью Маркова с непрерывным временем. Если все распределения вырождены в одной точке, то получают цепь Маркова с дискретным временем. за время [0, t].
за время [0, t].