|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯЗначение ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯ в математической энциклопедии: комплекснозначная функция j на группе G, удовлетворяющая неравенству для любых наборов Причина выделения этого класса функций состоит в том, что именно П. о. ф. определяют положительные функционалы на групповой алгебре тогда для положительности fj необходимо и достаточно, чтобы j была П. о. ф. Далее, fj определяет *-представление алгебры Если G- топологич. группа, то представление pj слабо непрерывно тогда и только тогда, когда П. о. ф. непрерывна. Если Gлокально компактна, то непрерывные П. о. ф. взаимно однозначно соответствуют положительным функционалам на L1(G). Для коммутативных локально компактных групп класс П. о. ф. совпадает с классом преобразований Фурье конечных положительных мер на двойственных группах. Имеется аналог этого утверждения для компактных групп: непрерывная функция j на компактной группе Gявляется П. о. ф. тогда и только тогда, когда ее преобразование Фурье для всякого представления s и всякого вектора Лит.:[1] Xьюитт Э., Росс К., Абстрактный гармонический анализ, пер. с англ., т. 2, М., 1975; [2] Наймарк М. А., Нормированные кольца, 2 изд., М., 1968. В. С. Шулъман. |
|
|
|

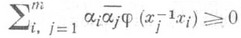
 Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного сопряжения.
Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного сопряжения. и унитарные представления группы G. Точнее, пусть
и унитарные представления группы G. Точнее, пусть  - произвольная функция и
- произвольная функция и  - функционал, заданный равенством
- функционал, заданный равенством 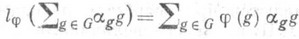
 в гильбертовом пространстве Hj и, следовательно, унитарное представление pj группы G, причем
в гильбертовом пространстве Hj и, следовательно, унитарное представление pj группы G, причем  для нек-рого
для нек-рого  . Обратно, Для любого представления p и любого вектора
. Обратно, Для любого представления p и любого вектора 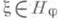 функция
функция  является П. о. ф.
является П. о. ф. принимает положительные (операторные) значения на каждом элементе двойственного объекта, т, е.
принимает положительные (операторные) значения на каждом элементе двойственного объекта, т, е.