|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛНЫЙ ОПЕРАТОРЗначение ПОЛНЫЙ ОПЕРАТОР в математической энциклопедии: - обобщенный волновой оператор, т. е. частично изометрич. оператор, определяемый равенством где А 1 и А 2 - самосопряженные операторы в сепара-бельном гильбертовом пространстве H, Р 1 - ортопроектор на H1, aс, и такой, что Здесь H1, aс, i=1, 2,-совокупность всех спектрально абсолютно непрерывных относительно Ai элементов х, т. е. таких, что спектральная мера Если оператор W+( А 2, A1).(или аналогично определяемый оператор W-(A2, А 1)).существует и является полным, то Ai, aс- части операторов Ai на Hi, aс унитарно эквивалентны. Если A1 и А 2 - самосопряженные операторы в H и Лит.:[1] Като Т., Теория возмущений линейных операторов, пер. с англ., М., 1972. В. И. Соболев. |
|
|
|

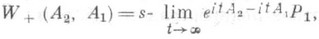
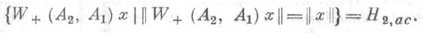
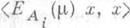 множества Мабсолютно непрерывна относительно меры Лебега m (x).
множества Мабсолютно непрерывна относительно меры Лебега m (x).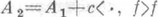 , где
, где 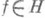 и с вещественно, то W+(A2, A1).и W+(A1, А 2).существуют и являются полными.
и с вещественно, то W+(A2, A1).и W+(A1, А 2).существуют и являются полными.