|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛНОЕ РИМАНОВО ПРОСТРАНСТВОЗначение ПОЛНОЕ РИМАНОВО ПРОСТРАНСТВО в математической энциклопедии: риманово пространство с функцией расстояния r, полное как метрич. пространство с метрикой r. Пусть М - связное риманово пространство со связностью Леви-Чивита, тогда следующие три утверждения эквивалентны: а) М - полно; б) для каждой точки Имеется [2] обобщение этой теоремы на случай пространства с несимметричной функцией расстояния. Лит.:[1] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [2] Кон-Фоссен С. Э., Некоторые вопросы дифференциальной геометрии в целом, М., 1959. М. И. Войцеховский. |
|
|
|

 экспоненциальное отображение ехр p определено на всем М р (где М р - касательное пространство и Мв р);в) каждое ограниченное по отношению к расстоянию r замкнутое множество
экспоненциальное отображение ехр p определено на всем М р (где М р - касательное пространство и Мв р);в) каждое ограниченное по отношению к расстоянию r замкнутое множество 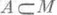 компактно (теорема Хопфа - Ринова). Следствия: любые две точки р,
компактно (теорема Хопфа - Ринова). Следствия: любые две точки р, П. р. п. можно соединить на Мгеодезич. длины r( р, q);любая геодезическая неограниченно продолжаема.
П. р. п. можно соединить на Мгеодезич. длины r( р, q);любая геодезическая неограниченно продолжаема.