"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЛНАЯ ГРУППАЗначение ПОЛНАЯ ГРУППА в математической энциклопедии:
- группа, в к-рой для любого ее элемента gи любого целого числа 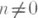 разрешимо уравнение х п=g. Абелева П. г. наз. также делимой группой. Важными примерами П. г. являются аддитивная группа всех рациональных чисел и группа всех комплексных корней из 1 степеней р k, k=l, 2, . . ., где p - простое число (квазициклическая группа). Всякая абелева П. г. разлагается в прямую сумму групп, каждая из к-рых изоморфна одной из указанных. О неабелевых П. г. известно значительно меньше. Всякая неединичная П. г. бесконечна. Всякая группа вложима в подходящую П. г. Если в П. г. указанные в определении уравнения разрешимы однозначно, она наз. D- группой. Таковы, в частности, локально нильпотентные П. г. без кручения. разрешимо уравнение х п=g. Абелева П. г. наз. также делимой группой. Важными примерами П. г. являются аддитивная группа всех рациональных чисел и группа всех комплексных корней из 1 степеней р k, k=l, 2, . . ., где p - простое число (квазициклическая группа). Всякая абелева П. г. разлагается в прямую сумму групп, каждая из к-рых изоморфна одной из указанных. О неабелевых П. г. известно значительно меньше. Всякая неединичная П. г. бесконечна. Всякая группа вложима в подходящую П. г. Если в П. г. указанные в определении уравнения разрешимы однозначно, она наз. D- группой. Таковы, в частности, локально нильпотентные П. г. без кручения.
Лит.:[1] Курош А. Г., Теория групп, 3 изд., М., 1967; [2] Каргаполов М. И., Мерзляков Ю. И., Основы теории групп, 3 изд., М., 1982. А. Л. Шмелькин.
|

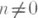 разрешимо уравнение х п=g. Абелева П. г. наз. также делимой группой. Важными примерами П. г. являются аддитивная группа всех рациональных чисел и группа всех комплексных корней из 1 степеней р k, k=l, 2, . . ., где p - простое число (квазициклическая группа). Всякая абелева П. г. разлагается в прямую сумму групп, каждая из к-рых изоморфна одной из указанных. О неабелевых П. г. известно значительно меньше. Всякая неединичная П. г. бесконечна. Всякая группа вложима в подходящую П. г. Если в П. г. указанные в определении уравнения разрешимы однозначно, она наз. D- группой. Таковы, в частности, локально нильпотентные П. г. без кручения.
разрешимо уравнение х п=g. Абелева П. г. наз. также делимой группой. Важными примерами П. г. являются аддитивная группа всех рациональных чисел и группа всех комплексных корней из 1 степеней р k, k=l, 2, . . ., где p - простое число (квазициклическая группа). Всякая абелева П. г. разлагается в прямую сумму групп, каждая из к-рых изоморфна одной из указанных. О неабелевых П. г. известно значительно меньше. Всякая неединичная П. г. бесконечна. Всякая группа вложима в подходящую П. г. Если в П. г. указанные в определении уравнения разрешимы однозначно, она наз. D- группой. Таковы, в частности, локально нильпотентные П. г. без кручения.