"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕРГМАНА - ВЕЙЛЯ ПРЕДСТАВЛЕНИЕ
Значение БЕРГМАНА - ВЕЙЛЯ ПРЕДСТАВЛЕНИЕ в математической энциклопедии:
Бергмана- Вейля формула, Вейля формула,- интегральное представление голоморфных функций, полученное А. Вейлем и С. Бергманом (см.[1], [2]) и определяемое следующим образом. Пусть  - область голоморфности в
- область голоморфности в  , функции
, функции  голоморфны в
голоморфны в  и
и 
Тогда любую функцию  голоморфную в
голоморфную в  и непрерывную в
и непрерывную в  в любой точке
в любой точке  , можно представить формулой
, можно представить формулой

где суммирование производится по всем  а интегрирование - по соответствующим образом ориентированным
а интегрирование - по соответствующим образом ориентированным  -мерным поверхностям образующим остов области
-мерным поверхностям образующим остов области  (см. Аналитический
(см. Аналитический полиэдр),
полиэдр),  а функции
а функции  голоморфны в области
голоморфны в области  и определяются в соответствии с Xефера теоремой (см. [3], с. 245) из равенств
и определяются в соответствии с Xефера теоремой (см. [3], с. 245) из равенств

Интегральное представление (*) наз. представлением Бергмана- Вейля.
Области V, фигурирующие в Б.- В. п., наз. областями Вейля; обычно для них требуется дополнительное условие, чтобы ранги матриц  ,
,  на соответствующих множествах
на соответствующих множествах

были максимальными  для всех
для всех  (такие области Вейля наз. регулярными). Области Вейля в Б.- В. п. можно заменить аналитическими полиэдрами
(такие области Вейля наз. регулярными). Области Вейля в Б.- В. п. можно заменить аналитическими полиэдрами

где  - ограниченные области с кусочно гладкими границами
- ограниченные области с кусочно гладкими границами  на плоскости
на плоскости  . Б,- В. п. определяет значение голоморфной функции
. Б,- В. п. определяет значение голоморфной функции  внутри аналитич. олиэдра
внутри аналитич. олиэдра  по значениям
по значениям  на его остове
на его остове  ; при
; при  размерность
размерность 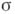 строго меньше размерности
строго меньше размерности  . При
. При  аналитич. олиэдры вырождаются в области с кусочно гладкими границами, остов и граница совпадают, а если еще
аналитич. олиэдры вырождаются в области с кусочно гладкими границами, остов и граница совпадают, а если еще  и
и  , то Б.- В. п. совпадает с интегральной формулой Коши.
, то Б.- В. п. совпадает с интегральной формулой Коши.
Важным свойством Б,- В. П. является голоморфность (по  ) его ядра. Поэтому если вместо голоморфной функции
) его ядра. Поэтому если вместо голоморфной функции  поставить произвольную интегрируемую на а функцию, то правая часть Б.- В. п. даст функцию, голоморфную всюду в
поставить произвольную интегрируемую на а функцию, то правая часть Б.- В. п. даст функцию, голоморфную всюду в  и почти всюду в
и почти всюду в  ; такие функции наз. интегралами типа Бергмана- Вейля. Если
; такие функции наз. интегралами типа Бергмана- Вейля. Если  голоморфна в
голоморфна в  и непрерывна в
и непрерывна в  , то ее интеграл типа Бергмана - Вейля равен нулю почти всюду в
, то ее интеграл типа Бергмана - Вейля равен нулю почти всюду в 
Из В.- В. п. в области Вейля  после замены
после замены

получается разложение Вейля

в ряд по функциям, голоморфным в области D, и этот ряд сходится равномерно на компактных подмножествах V.
Лит.:[1] WеilA., "Math. Ann.", 1935, Bd 111,8.178-82; [2] Bergman S., "Матем., сб.", 1936, т. 1, с. 242-57; [3] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964. Е. М. Чирка.

 - область голоморфности в
- область голоморфности в  , функции
, функции  голоморфны в
голоморфны в  и
и 
 голоморфную в
голоморфную в  и непрерывную в
и непрерывную в  в любой точке
в любой точке  , можно представить формулой
, можно представить формулой 
 а интегрирование - по соответствующим образом ориентированным
а интегрирование - по соответствующим образом ориентированным  -мерным поверхностям образующим остов области
-мерным поверхностям образующим остов области  (см. Аналитический
(см. Аналитический полиэдр),
полиэдр),  а функции
а функции  голоморфны в области
голоморфны в области  и определяются в соответствии с Xефера теоремой (см. [3], с. 245) из равенств
и определяются в соответствии с Xефера теоремой (см. [3], с. 245) из равенств 
 ,
,  на соответствующих множествах
на соответствующих множествах 
 для всех
для всех  (такие области Вейля наз. регулярными). Области Вейля в Б.- В. п. можно заменить аналитическими полиэдрами
(такие области Вейля наз. регулярными). Области Вейля в Б.- В. п. можно заменить аналитическими полиэдрами 
 - ограниченные области с кусочно гладкими границами
- ограниченные области с кусочно гладкими границами  на плоскости
на плоскости  . Б,- В. п. определяет значение голоморфной функции
. Б,- В. п. определяет значение голоморфной функции  внутри аналитич. олиэдра
внутри аналитич. олиэдра  по значениям
по значениям  на его остове
на его остове  ; при
; при  размерность
размерность 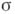 строго меньше размерности
строго меньше размерности  . При
. При  аналитич. олиэдры вырождаются в области с кусочно гладкими границами, остов и граница совпадают, а если еще
аналитич. олиэдры вырождаются в области с кусочно гладкими границами, остов и граница совпадают, а если еще  и
и  , то Б.- В. п. совпадает с интегральной формулой Коши.
, то Б.- В. п. совпадает с интегральной формулой Коши. ) его ядра. Поэтому если вместо голоморфной функции
) его ядра. Поэтому если вместо голоморфной функции  поставить произвольную интегрируемую на а функцию, то правая часть Б.- В. п. даст функцию, голоморфную всюду в
поставить произвольную интегрируемую на а функцию, то правая часть Б.- В. п. даст функцию, голоморфную всюду в  и почти всюду в
и почти всюду в  ; такие функции наз. интегралами типа Бергмана- Вейля. Если
; такие функции наз. интегралами типа Бергмана- Вейля. Если  голоморфна в
голоморфна в  и непрерывна в
и непрерывна в  , то ее интеграл типа Бергмана - Вейля равен нулю почти всюду в
, то ее интеграл типа Бергмана - Вейля равен нулю почти всюду в 
 после замены
после замены 
