|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОЗИЦИОННАЯ ИГРАЗначение ПОЗИЦИОННАЯ ИГРА в математической энциклопедии: - игра, имеющая характер развертывающегося в дискретном времени процесса на древовидно упорядоченном множестве (наз. также деревом). Конечной П. и. наз. система где 1) I - множество игроков (|I| = n); 2) X- конечное дерево, вершины к-рого наз. позициями, а корень - начальной позицией. Для позиций естественно определяется отношение следования; позиции, непосредственно следующие за данной - разбиение каждого Xi, i>0. Предполагается, что все позиции хиз данного Чистой стратегией игрока iв П. и. является функция, ставящая в соответствие каждому информационному множеству П. и. наз. игрой с полной информацией, если информационные множества игроков состоят из одной позиции каждое. В игре с полной информацией существует ситуация равновесия в чистых стратегиях (теорема Цермело - Неймана). Важную ролг" в П. и. играют смешанные стратегии. Две смешанные стратегии игрока наз. эквивалентными, если в ситуациях, отличающихся только этими стратегиями, вероятности каждой окончательной позиции равны. Игрок имеет полную память, если каждое его информационное множество следует за единственной альтернативой всех предшествующих информационных множеств этого игрока. Наличие полной памяти у игрока означает, что в момент совершения хода он помнит все информационные множества, в к-рых он находился, и свои выборы в них. Стратегией поведения наз. такая сметанная стратегия, при к-рой случайные выборы альтернатив информационных множеств стохастически независимы. Каждая смешанная стратегия игрока эквивалентна нек-рой стратегии поведения тогда и только тогда, когда игрок имеет полную память (теорема Куна). Более общими являются П. н. с бесконечным множеством альтернатив в каждой позиции и с бесконечно продолжающимися партиями, а также игры на графах. Лит.:[1] Позиционные игры, М., 1967; [2] Берж К., Общая теория игр нескольких лиц, пер. с франц., М., 1961; [3] Кун Г. У., в сб.: Позиционные игры, М., 1967, с. 13-40; [4] Thompson G. L., в кн.: Contributions to the theory of games, v. 2, Princeton, 1953, p. 267-77; [5] Воробьев Н. Н., "Проблемы кибернетики", 1962, в. 7, с. 5-20; [6] Буй Конг Кыонг, "Вестник ЛГУ", 1969, № 1, с. 49-59. Н. Я. Воробьев, А. Н. Ляпунов. |
|
|
|


 , наз. альтернативами х;позиции, не имеющие альтернатив, наз. окончательными, а ведущие в них пути - партиями; множество окончательных позиций обозначается X*;3)
, наз. альтернативами х;позиции, не имеющие альтернатив, наз. окончательными, а ведущие в них пути - партиями; множество окончательных позиций обозначается X*;3)  - разбиение множества ХХ* на n+1 множеств очередности Х 0, Х 1, ..., Х п. В позициях из Xi, i>0, ход осуществляется игроком i, в позициях из Х 0 - случайно; 4) Р х- вероятностные распределения на множествах альтернатив каждой позиции
- разбиение множества ХХ* на n+1 множеств очередности Х 0, Х 1, ..., Х п. В позициях из Xi, i>0, ход осуществляется игроком i, в позициях из Х 0 - случайно; 4) Р х- вероятностные распределения на множествах альтернатив каждой позиции 
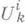 имеют одинаковое число альтернатив и никакие две из них не следуют друг за другом; множества
имеют одинаковое число альтернатив и никакие две из них не следуют друг за другом; множества  наз. информационными. Между альтернативами всех позиций одного информационного множества установлено однозначное соответствие, и каждый его класс наз. альтернативой самого информационного множества; 6) hi - функция, ставящая в соответствие каждой окончательной позиции выигрыш в ней игрока i.
наз. информационными. Между альтернативами всех позиций одного информационного множества установлено однозначное соответствие, и каждый его класс наз. альтернативой самого информационного множества; 6) hi - функция, ставящая в соответствие каждой окончательной позиции выигрыш в ней игрока i.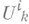 нек-рую его альтернативу. Набор пчистых стратегий всех игроков составляет ситуацию. Процесс игры в условиях сложившейся ситуации можно понимать как случайное блуждание по множеству позиций от начальной позиции к окончательной, причем в каждой позиции игрок, множеству очередности к-рого принадлежит эта позиция, знает лишь содержащее ee информационное множество и выбирает альтернативу в соответствии со своей стратегией. В позициях из Х 0 выбор альтернативы случаен. Это случайное блуждание определяет вероятностное распределение на множестве окончательных позиций. Принимая за выигрыш игрока математич. ожидание его выигрыша на окончательных позициях, получают бескоалиционную игру в нормальной форме.
нек-рую его альтернативу. Набор пчистых стратегий всех игроков составляет ситуацию. Процесс игры в условиях сложившейся ситуации можно понимать как случайное блуждание по множеству позиций от начальной позиции к окончательной, причем в каждой позиции игрок, множеству очередности к-рого принадлежит эта позиция, знает лишь содержащее ee информационное множество и выбирает альтернативу в соответствии со своей стратегией. В позициях из Х 0 выбор альтернативы случаен. Это случайное блуждание определяет вероятностное распределение на множестве окончательных позиций. Принимая за выигрыш игрока математич. ожидание его выигрыша на окончательных позициях, получают бескоалиционную игру в нормальной форме.