|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПОДМНОГООБРАЗИЕЗначение ПОДМНОГООБРАЗИЕ в математической энциклопедии: - 1) В узком смысле слова топологическое n-мерное П. топологического m-мерного многообразия М - такое подмножество 2) В широком смысле слова топологическое n-мерное П. топологического m-мерного многообразия М - такое n-мерное многообразие N, к-рое как множество точек является подмножеством М(иными словами, N - это подмножество М, снабженное структурой п- мерного многообразия) и для. к-рого тождественное вложение 3) Кусочно линейное, аналитическое или дифференцируемое (класса В аналитическом и дифференцируемом случаях П. всегда является локально плоским. Поэтому определение аналитического (дифференцируемого) П. в узком смысле обычно с самого начала формулируется как аналитический (дифференцируемый) вариант данного в 1) определении локально плоского П. с помощью локальных координат, добавляя к сказанному там условию, чтобы локальные координаты x1, . . ., х т были аналитическими (дифференцируемыми класса С l). Если подмножество Nудовлетворяет последнему определению, то оно естественным образом снабжается структурой аналитического (дифференцируемого класса С l).многообразия и iоказывается вложением в смысле соответствующей структуры. Кусочно линейное П. в узком смысле локально представляется как подполиэдр объемлющего многообразия, кусочно линейно эквивалентный симплексу. Оно не всегда является локально плоским (хотя это так при т - n>2); кроме того, для таких П. свойство быть локально плоским в топологич. смысле не совпадает (по крайней мере непосредственно) со свойством быть локально плоским в кусочно линейном смысле. 4) Простой модификацией этих определений получаются определения: П. с краем; П. многообразия с краем (при этом в ряде топологич. вопросов оказывается целесообразным ограничить возможные расположения П. у края объемлющего многообразия, см. [1]); П., различные компоненты к-рого могут иметь различную размерность; П. бесконечномерного многообразия [2]; комплексно аналитического П. комплексно аналитического многообразия. Понятие П. в узком смысле является непосредственным обобщением понятия кривой и поверхности. П. в широком смысле используются в теории групп Ли (где это понятие и было впервые введено [3]), дифференциальной геометрии [4] и теории слоений. 5) В алгебраической геометрии П.- замкнутое подмножество алгебраич. многообразия в Зариского топологии. Этим формализуется идея, что П. задается алгебраич. уравнениями. Помимо перехода от R к другим полям, изменение понятия П. в этом случае состоит в том, что допускаются П. с особенностями. Лит.:[1] Рохлин В. А., Фукс Д. Б., Начальный курс топологии. Геометрические главы, М., 1977; [2] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; [3] Шевалле К., Теория групп Ли, пер. с англ., т. 1, М., 1948; [4] Стернберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970. Д. В. Аносов. |
|
|
|

 , к-рое в индуцированной топологии является n-мерным многообразием. Число m - nназ. коразмерностью подмногообразия N. Наиболее часто встречаются локально плоские П., для к-рых тождественное вложение
, к-рое в индуцированной топологии является n-мерным многообразием. Число m - nназ. коразмерностью подмногообразия N. Наиболее часто встречаются локально плоские П., для к-рых тождественное вложение  является локально плоским вложением. Подмножество
является локально плоским вложением. Подмножество  является локально плоским П., если для каждой точки
является локально плоским П., если для каждой точки  имеются такая окрестность Uэтой точки в Ми такие локальные координаты x1,. . ., xm в ней, что в терминах этих координат
имеются такая окрестность Uэтой точки в Ми такие локальные координаты x1,. . ., xm в ней, что в терминах этих координат  описывается уравнениями xn+1=...=xm=0.
описывается уравнениями xn+1=...=xm=0.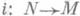 является погружением. П. в узком смысле является П. в широком смысле, а последнее является П. в узком смысле тогда и только тогда, когда iесть вложение в топологич. смысле (т. е. у каждой точки
является погружением. П. в узком смысле является П. в широком смысле, а последнее является П. в узком смысле тогда и только тогда, когда iесть вложение в топологич. смысле (т. е. у каждой точки  имеется сколь угодно малые окрестности в N, являющиеся пересечениями с N нек-рых окрестностей в М).
имеется сколь угодно малые окрестности в N, являющиеся пересечениями с N нек-рых окрестностей в М). ) П. кусочно линейного, аналитического или дифференцируемого (класса
) П. кусочно линейного, аналитического или дифференцируемого (класса  ) многообразия Мв широком смысле (соответственно узком) - это подмножество
) многообразия Мв широком смысле (соответственно узком) - это подмножество  , к-рое снабжено структурой кусочно линейного, аналитического или дифференцируемого (класса С l).многообразия, причем iявляется кусочно линейным, аналитическим или дифференцируемым (класса С l).погружением (соответственно вложением). Определение дифференцируемого П. класса С l годится и при l=0, совпадая в этом случае с определением топологического П. Обычно подразумевается, что
, к-рое снабжено структурой кусочно линейного, аналитического или дифференцируемого (класса С l).многообразия, причем iявляется кусочно линейным, аналитическим или дифференцируемым (класса С l).погружением (соответственно вложением). Определение дифференцируемого П. класса С l годится и при l=0, совпадая в этом случае с определением топологического П. Обычно подразумевается, что  .
.